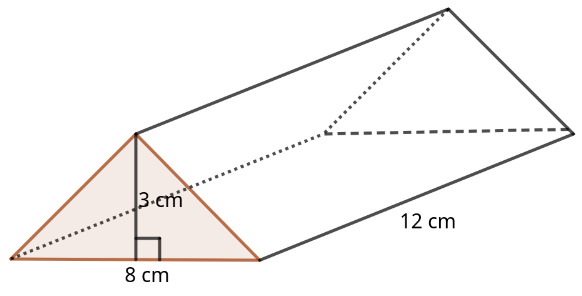
Activity 2.7.8.
Formula of the surface area of a triangular prism is the sum of:
1. Two triangular bases
\begin{align*}
\text{Area of a triangle} = \amp \frac{1}{2} \times \text{base} \times \text{height} \\
\text{Total area for two triangles} \\
= \amp 2 \times (\frac{1}{2} \times \text{base} \times \text{height}) \\
= \amp b \times h
\end{align*}
2.Two rectangular lateral faces
The three faces depend on the perimeter of the triangular base and the prism length \(L\)
\begin{align*}
\text{Lateral Area} = \amp \text{Base Area} \times \text{Lateral Area} \\
=\amp (b \times h) + (\text{Perimeter} \times L)
\end{align*}
Total Surface Area formula:
\begin{align*}
S.A =\amp \text{Base Area} \times \text{Lateral Area}
\end{align*}