Skip to main content
Contents Dark Mode Prev Up Next \(\newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Subsection 2.1.3 Scale Factors
Scale factor is a fundamental concept in mathematics, especially in geometry, where it is used to describe the proportional relationship between similar figures.
It is defined as the ratio of corresponding side lengths in two similar shapes.
Understanding scale factor helps students grasp how objects are enlarged or reduced while maintaining their shape and proportions.
Subsubsection 2.1.3.1 Area Scale Factor
Activity 2.1.3 .
(a) Draw a square with a side length of
\(4\) cm and label it as Square
\(A\) as shown below.
(b) Draw another square with a side length of
\(8\) cm and label it as Square
\(B\) as shown below.
(c) Calculate the area of Square
\(A\) and Square
\(B\text{.}\)
(d) Find the ratio of the areas by dividing the area of Square
\(B\) by the area of Square
\(A\text{.}\)
(e) Take one side length of Square
\(B\text{,}\) divide it by one side length of Square
\(A\text{,}\) and then square the result.
(f) Compare your answers from steps
\((\mathbf{d})\) and
\((\mathbf{e})\text{.}\) What do you notice?
(g) Discuss and share your findings with the rest of the class.
\(\textbf{Key Takeaway}\)
Area scale factor is the ratio of the area of the image to area of the object.
Area scale factor is the square of linear scale factor.
In the Figures below, the parallelogram
\(P'Q'R'S'\) represents the enlarged image of paralellogram
\(PQRS\text{,}\) transformed by a scale factor of
\(2\text{.}\)
\begin{align*}
\text{Area of a parallelogram}= \amp base \times height \\
\text{Area of PQRS} =\amp 5\, cm \times 7\, cm \\
= \amp 35\, cm^2\\
\text{Area of P'Q'R'S'}= \amp 10\, cm \times 14\, cm\\
= \amp 140\, cm^2\\
\text{Area scale factor}= \amp \frac{\text{Area of the image}}{\text{area of the object}}\\
\frac{\text{Area of P'Q'R'S'}}{\text{Area of PQRS}}= \amp \frac{140\, cm^2}{35\, cm^2}\\
= \amp 4
\end{align*}
Example 2.1.23 .
A square whose area is
\(28\) \(cm^2\) is given an enlargement with a linear scale factor of
\(4\text{.}\) Find the area of the image.
Solution .
\begin{align*}
\text{Area scale factor}= \amp \frac{\text{Area of image}}{\text{area of object}}\\
\text{Linear scale factor (L.S.F)}= \amp 4\\
\text{Area scale factor(A.S.F)} =\amp (L.S.F)^2\\
= \amp4^2 =16 \\
\frac{\text{Area of image}}{28} =\amp 16 \\
\text{Area of image}= \amp 16 \times 28\\
= \amp 448\, cm^2
\end{align*}
Example 2.1.24 .
Given that the ratio of the area of two circles is
\(\frac{25}{64}\text{.}\)
(a). Find the ratio of their radii
(b). If the smaller one has a radius of
\(15\) \(\, cm\text{,}\) find the radius of the larger one.
Solution .
\begin{align*}
\text{(a)Area scale factor} =\amp \frac{25}{64}\\
\text{Linear scale factor}= \amp \sqrt \frac {25}{64}\\
= \amp \frac{5}{8}\\
\text{Therefore the ratio of two radii}= \amp 5:8
\end{align*}
(b).If the radius of the smaller circle is
\(15 \, cm\text{,}\) then
\begin{align*}
\frac{\text{Radius of smaller circle}}{\text{Radius of larger circle}}= \amp \frac{5}{8}\\
\frac{15}{\text{radius of larger circle}} =\amp \frac{5}{8} \\
\text{radius of larger circle}= \amp \frac{(8 \times 15)}{5} \\
= \amp 24\, cm
\end{align*}
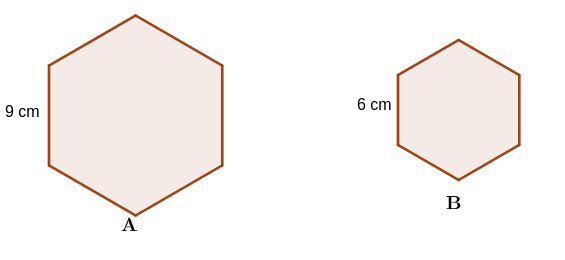
Example 2.1.25 .
Given that the following two hexagons below are similar, and the area of the first hexagon
\(A\) is
\(450\, cm^2\text{,}\) calculate the area of the second hexagon
\(B\text{.}\)
Solution .
\begin{align*}
\text{Linear scale factor}= \amp \frac{9}{6}\\
\text{Area scale factor}= \amp (\frac{9}{6})^2=\frac{81}{36}\\
\frac{\text{Area of hexagon A}}{\text{Area of hexagon B}} =\amp\frac{81}{36} \\
\frac{\text{450}}{\text{Area of hexagon B}} =\amp\frac{81}{36} \\
\text{Area of hexagon B} =\amp \frac{36\times 450}{81}\\
= \amp 200 cm^2
\end{align*}
Checkpoint 2.1.26 . Finding the Area of a Similar Polygon.
Load the question by clicking the button below.
Checkpoint 2.1.27 . Finding the Area of a Smaller Cone.
Load the question by clicking the button below.
Checkpoint 2.1.28 . Relationship Between Side Lengths and Areas.
Load the question by clicking the button below.
Exercises Exercises
1. The corresponding sides of two similar regular hexagons are
\(4\, cm\) and
\(9\, cm\) respectively.
(a).Find the ratio of their areas.
(b).Calculate the area of the larger hexagon if the area of the smaller hexagon is
\(64\, cm^2\text{.}\)
2. The ratio of the area of two similar cones is
\(\frac{9}{36}\text{.}\)
(a).Find the area of the smaller cone if the area of the bigger cone is
\(320\, m^2\)
(b). Find the ratio of their base radii.
(c). If the slanting height of the smaller cone is
\(7\, m\text{,}\) find the slanting height of the larger cone.
3. The length of a parallelogram is
\(15\, cm\) and its area is
\(240\, cm^2\text{.}\) Calculate the length of a similar parallelogram whose area is
\(375\, cm^2\text{.}\)
4. The area of a circle is
\(49\, m^2\) . A second circle has a radius that is
\(4\) times the radius of the first circle. What is the area of the second circle?
Subsubsection 2.1.3.2 Volume Scale Factor
Activity 2.1.4 .
(a) Draw a cuboid with dimensions
\(8\) cm (length),
\(5\) cm (width), and
\(4\) cm (height), and label it as Cuboid
\(A\) as shown below.
(b) Draw another cuboid with dimensions
\(24\) cm (length),
\(15\) cm (width), and
\(12\) cm (height), and label it as Cuboid
\(B\) as shown below.
(c) Calculate the volume of each cuboid by multiplying length
\(\times\) width
\(\times\) height.
(d) Find the volume ratio by dividing the volume of Cuboid
\(B\) by the volume of Cuboid
\(A\text{.}\)
(e) Find the ratio of the length of Cuboid
\(B\) to the length of Cuboid
\(A\text{,}\) then raise the result to the power of three
(f) Calculate the ratio by dividing the width of Cuboid
\(B\) by the width of Cuboid
\(A\text{,}\) then cube the resulting value
(g) Determine the ratio by dividing the height of Cuboid
\(B\) by the height of Cuboid
\(A\text{,}\) then cube the resulting value.
(h) Compare the result obtained from step
\(\textbf{d}\) with the values calculated in steps
\(\textbf{e}\text{,}\) \(\textbf{f}\text{,}\) and
\(\textbf{g}\text{.}\) Note any patterns or relationships you observe among these results.
(i) Discuss and share the results with the rest of the learners in the class.
\(\textbf{Key Takeaway}\)
A volume scale factor is the cube of the linear scale factor, representing the ratio by which the volume of a scaled object changes compared to the original object.
Example 2.1.29 .
The corresponding heights of two similar cylinders are
\(4\, m\) and
\(5\, m\text{.}\)
(a). Find the ratio of their corresponding volumes.
(b).If the smaller cylinder has a volume of
\(1536\, m^3\text{,}\) find the volume of the larger cylinder.
Solution .
\begin{align*}
\text{(a).The ratio of the heights}= \amp \frac{4}{5}\\
\text{Linear scale factor}= \amp \frac{4}{5}\\
\text{Volume scale factor} =\amp (L.S.F)^3\\
= \amp \left( \frac{4}{5} \right)^3\\
= \amp \frac{64}{125}\\
\text{Therefore ratio of the volumes } =\amp 64:125\\
\text{(b). Volume of larger cylinder;} \amp \\
\frac{\text{Volume of smaller cylinder}}{\text{volume of larger cylinder}} =\amp \text{volume scale factor}\\
\frac{1536}{\text{Volume of larger cylinder}}= \amp \frac{64}{125}\\
\text{Volume of larger cylinder}= \amp \frac{(125 \times 1546)}{64}\\
= \amp 3000\, m^3
\end{align*}
Example 2.1.30 .
The capacity of two similar containers are
\(288\, cm^3\) and
\(4500\, cm^3\text{.}\) Find the ratio of their:
(b). If the area of the smaller container is
\(140\, cm^2\text{,}\) find the area of the larger container.
Solution .
\begin{align*}
\text{Volume scale factor} =\amp \frac{288\, cm^3}{4500\, cm^3}=\frac{8}{125}\\
\text{Lenear scale factor}= \amp \sqrt[3]{\frac{8}{125}}.\\
= \amp \frac{2}{5}\\
\text{Therefore the ratio of the heights} =\amp 2:5
\end{align*}
\begin{align*}
\text{Area scale factor} =\amp \left( \frac{2}{5} \right)^2\\
= \amp \frac{4}{25}\\
\text{Area scale factor} =\amp \frac{\text{Area of the smaller container}}{\text{Area of the larger container}}\\
\frac{4}{25} =\amp \frac{140}{\text{Area of larger container}}\\
\text{Area of larger container} =\amp \frac{(25 \times 140)}{4}\\
= \amp 875\\
\text{The area of larger container}= \amp 875\, cm^2
\end{align*}
Example 2.1.31 .
Given that cone
\(A\) and cone
\(B\) are similar cones, and the volume of cone
\(A\) is
\(150 cm^3\text{,}\) calculate the volume of cone
\(B\text{.}\)
Solution .
\begin{align*}
\text{Linear scale factor} =\amp \frac{7}{21}=\frac{1}{3}\\
\text{Volume scale factor}= \amp(\frac{1}{3})^3=\frac{1}{27} \\
\frac{\text{Volume of cone A}}{\text{Volume of cone B}} =\amp\frac{1}{27} \\
\frac{150}{\text{Volume of cone B}}= \amp \frac{1}{27}\\
\text{Volume of cone B}= \amp 27 \times 150\\
= \amp 4050 cm^3
\end{align*}
Checkpoint 2.1.32 . Similar Pyramids (28-2).
Load the question by clicking the button below.
Checkpoint 2.1.33 . Finding the Capacity of a Larger Container.
Load the question by clicking the button below.
Checkpoint 2.1.34 . Finding the Height of a Larger Can.
Load the question by clicking the button below.
Checkpoint 2.1.35 . Ratio of Volumes of Similar Solids.
Load the question by clicking the button below.
Checkpoint 2.1.36 . Similarity and Enlargement - Cylinders.
Load the question by clicking the button below.
Exercises Exercises
1. Two similar containers have heights of
\(6\, cm\) and
\(9\,cm\text{,}\) respectively. If the smaller container holds
\(400\, ml\text{,}\) what is the capacity of the larger container?
2. Two similar cans have volumes of
\(192\, cm^3\) and
\(648\, cm^3\) respectively. If the smaller can has a height of
\(14\, cm\text{,}\) what is the height of the larger can?
3. The ratio of the lengths of the corresponding sides of two similar rectangular tanks is
\(3:5\text{.}\) The volume of the smaller tank is
\(8\, cm^3\text{.}\) Calculate the volume of the larger tank.
4. A small cube has a length of
\(3\, cm\text{.}\) A larger cube is created by scaling the small cube, such that each side of the larger cube is
\(6\) times the length of the corresponding side of the small cube.
(a).What is the volume of the small cube?
(b).What is the volume of the larger cube?
(c). By what factor has the volume increased when the small cube is scaled to the larger cube?
Reading Questions 2.1.3.3 Further Exercise
1. An architect is creating a scale model of a building. The actual height of the building is
\(120\) meters, and the height of the model is
\(0.6\) meters.
(a) What is the scale factor of the model?
(b) If the width of the actual building is
\(50\) meters, what is the width of the model?
2. A map scale is given as
\(1:25,000\text{,}\) meaning
\(1\, cm\) on the map represents
\(25,000\, cm\) in real life.
(a) A river on the map measures
\(8\, cm\) in length. What is the actual length of the river in kilometers?
(b) If a road on the map measures
\(12.5\, cm\text{,}\) how long is the actual road in meters?
3. A photograph has a size of
\(5\, cm\) by
\(7\, cm\text{.}\) It needs to be enlarged so that the width becomes
\(20\, cm\text{.}\) The height will also increase proportionally. What is the new height of the photograph after the enlargement?
4. A pole of height
\(2.4\) meters casts a shadow of length
\(1.6\) meters. A tree casts a shadow of length
\(12\) meters.
(a) Using the concept of similar triangles, find the height of the tree.
(b) If the tree’s shadow increases to
\(15\) meters, what would be the new height of the tree, assuming the proportion remains the same?