Skip to main content

Grade 10 Mathematics Learners’ Book

INNODEMS

Subsection 2.3.2 Rotation on Different Planes

Rotation on different planes" refers to the concept of rotating an object or point around various axes within different planes in a three-dimensional space.
🔗

Subsubsection 2.3.2.1 Rotation in the Cartesian Plane

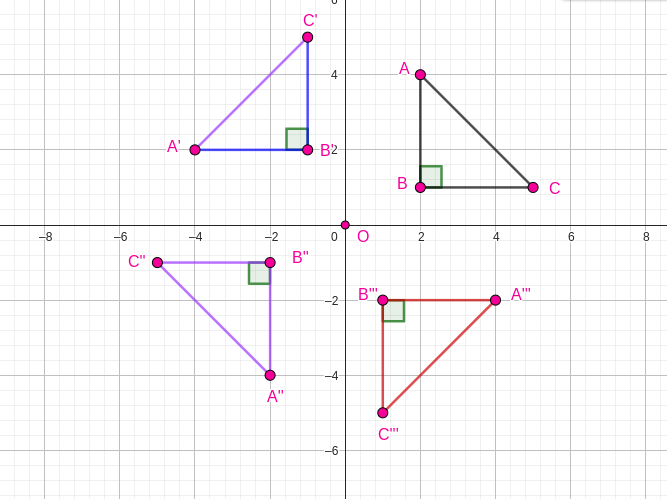
Activity 2.3.3.

Work in pairs
🔗
(a)
Draw a large \(X-\) axis (horizontal) and \(Y-\) axis (Vertical) on a graph of paper. Mark the origin \((0,0)\) where the two axis meet.
🔗
🔗
(b)
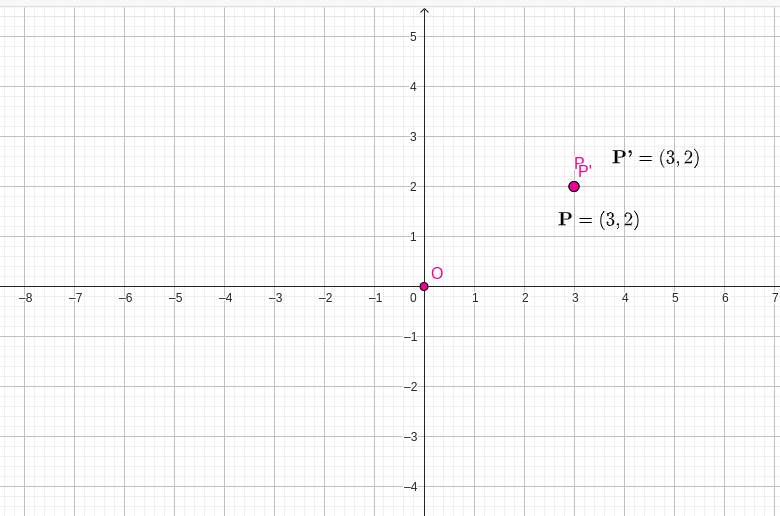
Pick any point \(P\, (x,y)\) and plot this point on the plane and label it for example let;s use \(P\, (3,2)\text{.}\)
🔗
🔗
(c)
Rotate the point in a counterclockwise direction around the origin with different angles as shown below:
🔗
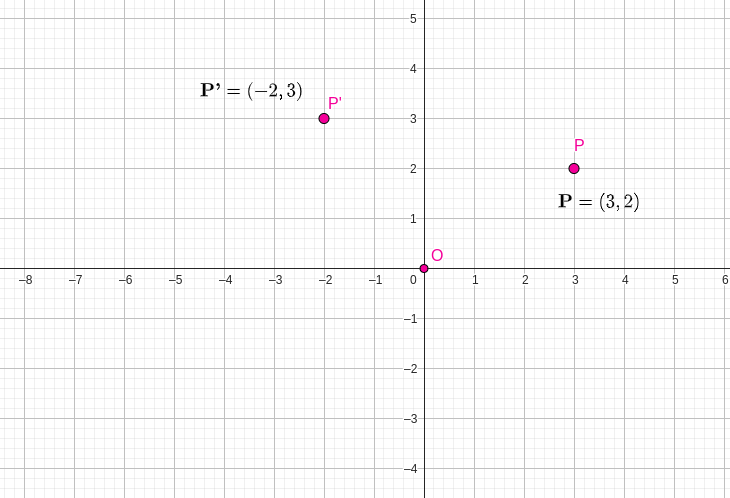
\begin{equation*} (i) \textbf{+90°} \end{equation*}
🔗
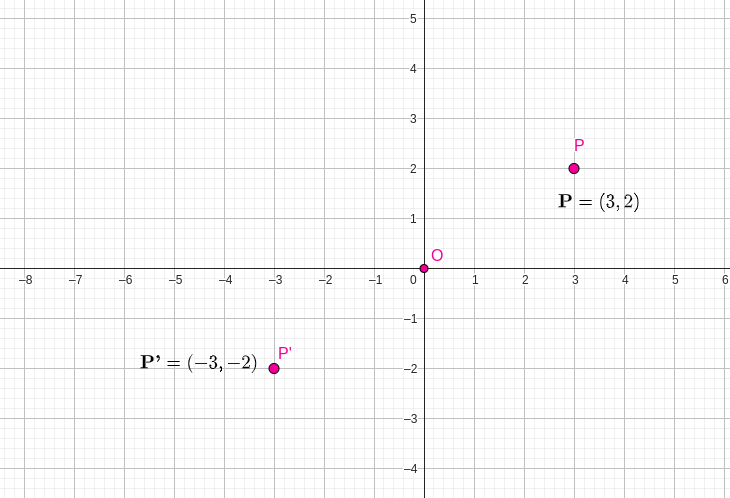
\begin{equation*} (ii) \textbf{+180°} \end{equation*}
🔗
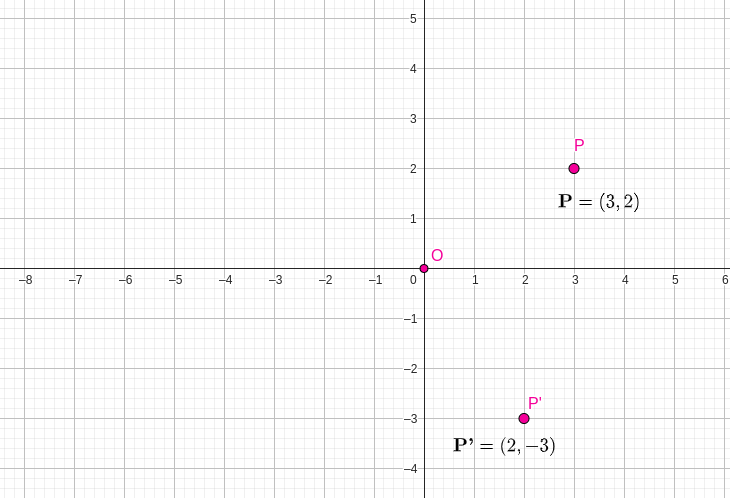
\begin{equation*} (iii) \textbf{+270°} \end{equation*}
🔗
\begin{equation*} (iv) \textbf{+360°} \end{equation*}
🔗
🔗
(d)
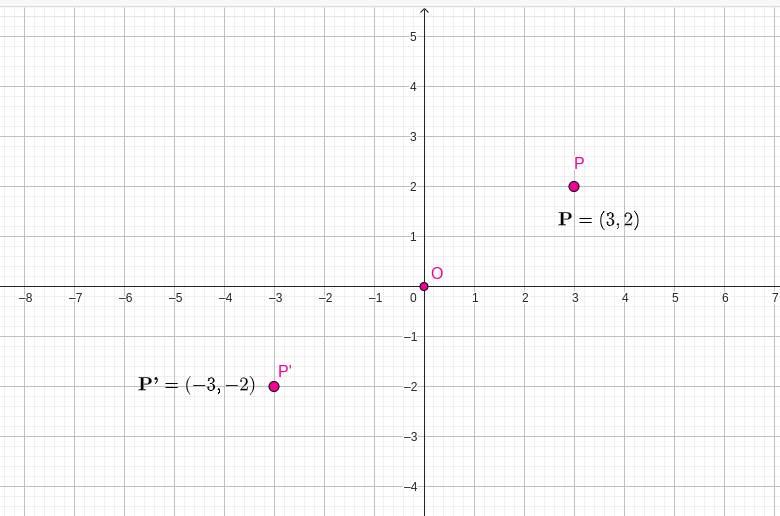
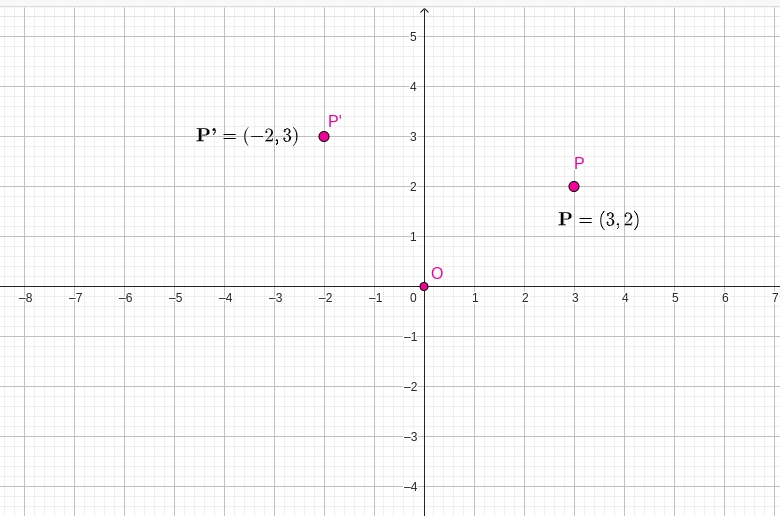
Similary rotate the point in a clockwise direction around the origin with different angles as shown below:
🔗
\begin{equation*} (i) \textbf{-90°} \end{equation*}
🔗
\begin{equation*} (ii) \textbf{=-180°} \end{equation*}
🔗
\begin{equation*} (iii) \textbf{-270°} \end{equation*}
🔗
\begin{equation*} (iv) \textbf{-360°} \end{equation*}
🔗
🔗
🔗
\(\textbf{Key Takeaway}\)
🔗
  1. The image of point \(P\) remains the same when rotated through \(\pm\, 180^\circ\) (clockwise or counterclockwise) about the origin.
    🔗
    🔗
  2. A rotation through \(\pm\, 360^\circ\) and \(0^\circ\) about the origin does not change the position of the object.
    🔗
    🔗
🔗
In summary, a point \((p,q)\) which is rotated through the indicated angles about the origin is shown in the table below.
🔗
Table 2.3.6.
🔗
\(\textbf{Angle of rotation}\) \(0^\circ\) \(+90^\circ\) \(-90^\circ\) \(180^\circ\) \(-180^\circ\) \(+270^\circ\) \(+360^\circ\) \(-360^\circ\)
\(\textbf{image of (p,q)}\) \((p,q)\) \((-q,p)\) \((q,-p)\) \((-p,-q)\) \((-p,-q)\) \((q,-p)\) \((p,q)\) \((p,q)\)
The figure below shows triangle \(ABC\) and its images after rotations about the origin with different angles of rotation (\(90^\circ\text{,}\) \(180^\circ\text{,}\) \(270^\circ\) and \(360^\circ\)).
🔗
Figure 2.3.7.
🔗
Table 2.3.8.
🔗
\(\textbf{Object}\) \(A\, (2,4)\) \(A\, (2,4)\) \(A\, (2,4)\) \(A\, (2,4)\) \(A\, (2,4)\) \(A\, (2,4)\) \(A\, (2,4)\) \(A\, (2,4)\)
\(B\, (2,1)\) \(B\, (2,1)\) \(B\, (2,1)\) \(B\, (2,1)\) \(B\, (2,1)\) \(B\, (2,1)\) \(B\, (2,1)\) \(B\, (2,1)\)
\(C\, (5,1)\) \(C\, (5,1)\) \(C\, (5,1)\) \(C\, (5,1)\) \(C\, (5,1)\) \(C\, (5,1)\) \(C\, (5,1)\) \(C\, (5,1)\)
\(\textbf{Angle of rotation}\) \(0^\circ\) \(+90^\circ\) \(-90^\circ\) \(+180^\circ\) \(-180^\circ\) \(270^\circ\) \(+360^\circ\) \(-360^\circ\)
\(\textbf{Image point}\) \(A\, (2,4)\) \(A'\, (-4,2)\) \(A\, (4,-2)\) \(A''\, (-2,-4)\) \(A''\, (-2,-4)\) \(A'''\, (4,-2)\) \(A\, (2,4)\) \(A\, (2,4)\)
\(B\, (2,1)\) \(B'\, (-1,2)\) \(B\, (1,-2)\) \(B''\, (-2-1)\) \(B''\, (-2,-1)\) \(B'''\, (1,-2)\) \(B\, (2,1)\) \(B\, (2,1)\)
\(C\, (5,1)\) \(C'\, (-1,5)\) \(C\, (1,-5)\) \(C''\, (-5-1)\) \(C''\, (-5,-1)\) \(C'''\, (1,-5)\) \(C\, (5,1)\) \(C\, (5,1)\)
\(\textbf{Rotation of Points by a Given Angle Around a Specified Center}\)
🔗
Consider a point \(A\, (4,3)\) .We are required to finding the coordinates of its image after a Rotation taking the centre to be \((1,2)\) and angle of rotation to be \(90^\circ\) ;
🔗
\((4,3)\) is mapped onto \((0,5)\text{.}\)
🔗
Given the point \((4,3)\) and the centre of rotation \((1,2)\text{,}\) To obtain this point \((0,5)\) without a graph, We follow this steps;
🔗
\begin{align*} \text{x-coordinate}= \amp 1-(3-2)=0\\ \text{y-coodinate}= \amp 2+(4-1)=5\\ \text{Point of the image}= \amp (0,5) \end{align*}
🔗
from the given points, for point \((4,3)\text{,}\)We let \(p=4\) and \(q=3\) and for the given centre \((1,2)\) we let \(x=1\) and \(y=2\text{.}\)
🔗
\(\textbf{In general a point (p,q) rotated through 90° about the centre (x,y) is mapped on to the point (x-(q-y)\, ,y+(p-x))}\)
🔗
Considering the same point \(P\text{,}\) but now the angle of rotation to be \(180^\circ\text{;}\) To find the coordinates of its image we follow the following steps:
🔗
Given the point \((4,3)\) and the centre of rotation \((1,2)\text{,}\) To find the point of the image we follow the following steps;
🔗
\begin{align*} \text{x-coordinate}= \amp (2 \times 1) -4\\ = \amp -2\\ \text{y-coordinate}= \amp (2 \times 2)-3\\ = \amp 1\\ \text{Point of the image}= \amp (-2,1) \end{align*}
🔗
\(\textbf{In general a point (p,q) rotated through 180° about the centre (x,y) is mapped on to the point (2x-p\, ,2y-q)}\)
🔗

Example 2.3.9.

A triangle \(ABC\) with coordinates \(A\,(2,1)\text{,}\) \(B\, (3,2)\) and \(C\, (3,4)\) is rotated through the centre and angle of \(90^\circ\) in a clockwise direction.Find the coordinates of its image
🔗
Solution.
Since triangle \(ABC\) is rotated in a clockwise direction with an angle of \(90^\circ\) through the origin, then the angle of rotation is \(-90^\circ\)
🔗
According to the rule, If we have our points \((p,q)\) which will be mapped to \((q,-p)\) if rotated through the centre and angle of rotation is \(-90^\circ\)
🔗
Therefore, we will individually apply the rotation formula to all three given points.
🔗
\begin{align*} A (2,1) \rightarrow\amp A'(1,-2)\\ B (3,2) \rightarrow\amp B'(2,-3)\\ C (3,4) \rightarrow\amp C'(4,-3) \end{align*}
🔗
The coordinates of triangle \(A'B'C'\) are \(A'\, (1,-2)\text{,}\) \(B'\, (2,-3)\) and \(C'\, (4,-3)\)
🔗
🔗
🔗

Exercises Exercises

1.
A point \(P\, (4,3)\) maps onto \(P'\, (-1,4)\) under a rotation R centre \((1,1)\text{.}\) Find the angle of rotation.
🔗
🔗
2.
Describe the rotation which maps the rectangle whose verticies are \(P\, (2,2)\text{,}\) \(Q\, (6,2)\text{,}\) \(R\,(6,4)\) and \(S\, (2,4)\) onto a rectangle whose verticies are \(P'\,(2,-2)\text{,}\) \(Q'\,(2,-6)\text{,}\) \(R'\,(4,-6)\) and \(S'\, (4,-2)\)
🔗
🔗
3.
Give the coordinates of the image of each of the following points when rotated through \(180^\circ\) in a clockwise direction about \((2,1)\)
🔗
(a) (4,-2)
🔗
(b) (-2,2)
🔗
(c) (4,4)
🔗
(d) (-2,-1)
🔗
(e) (-3,2)
🔗
🔗
4.
Find the coordinates of the verticies of the image of a triangle whose verticies are \(P\, (-4,6)\text{,}\) \(Q\, (-4,2)\) and \(R\, (-2,2)\) when rotated about the origin through:
🔗
(a) \(-90^\circ\)
🔗
(b) \(-180^\circ\)
🔗
(c) \(270^\circ\)
🔗
🔗
5.
The parallelogram whose verticies are \(A\, (4,4)\text{,}\) \(B\, (8,4)\text{,}\) \(C\, (2,2)\) and \(D\, (6,2)\) is rotated to give an image whose verticies are \(A'\, (4,-2)\text{,}\) \(B'\, (4,-6)\text{,}\) \(C'\, (2,0)\) and \(D'\, (2,-4)\text{.}\) Find the centre and angle of rotation.
🔗
🔗
🔗
🔗

Checkpoint 2.3.10.

🔗

Checkpoint 2.3.11.

🔗

Checkpoint 2.3.12.

🔗

Checkpoint 2.3.13.

🔗
🔗
PrevTopNext