Subsection 1.1.1 Classifying whole numbers as odd, even, prime and composite in different situations
Whole numbers can be classified as odd, even, prime or composite based on their divisibility and factor properties.
Activity 1.1.1.
-
Working in groups, write numbers from
\(1\) to
\(100\text{.}\)
-
Sort the numbers you wrote down into odd or even.
-
What patterns do you notice between even and odd numbers?
-
Identify prime and composite numbers from the list of even and odd numbers you have.
-
Discuss how a number is classified.
-
Identify prime numbers that are even.
-
Brainstorm a real life example where you can find odd, even, prime and composite numbers e.g pairs of shoes are even numbers.
-
Describe why classifying numbers in real-life could be useful.
-
Share your work with your fellow learners.
\(\textbf{Even and Odd numbers}\)
\(\textbf{Even numbers}\) are numbers that are divisible by
\(2\text{.}\)
\(\textbf{Odd numbers}\) are numbers that when divided by two, you get a remainder.
\(\textbf{Remark:}\) We can only talk about even and odd numbers if they are integers (i.e., elements of
\(\mathbb{Z}\)).
-
The sum or difference of two even numbers is even.
Example:
\(6 + 4 = 10\) and
\(6-2 = 4\text{.}\)
-
The sum or difference of two odd numbers is even.
Example:
\(7+3 = 10 \) and
\(11-9 = 2\)
-
The sum or difference of an even and an odd number is always odd.
Example:
\(8+ 5 = 13\) and
\(8-5 = 3\)
-
When two odd integers are multiplied, the result is always an odd number.
Example:
\(3 \times 3 = 9\)
-
When two even integers are multiplied, the result is an even number.
Example:
\(12 \times 12 = 144\) \(\)
-
An even number multiplied by an odd number equals an even number.
Example:
\(12 \times 3 = 36\)
\(\textbf{Criterion 1: How to Identify Even or Odd Integers}\)
A number is even if it ends with one of the digits:
\(0, 2, 4, 6, 8. \)
A number is odd if it ends with one of the digits:
\(1, 3, 5, 7, 9.\)
\(\textbf{Note}:\) This method works only for integers (whole numbers, including zero and negatives).
Example 1.1.1.
Classify the following numbers as even or odd:
Solution.
-
\(1107\) is an odd number since its last digit is
\(7\text{.}\)
-
\(2028\) is an even number since its last digit is
\(8\text{.}\)
-
\(3333\) is an odd number since its last digit is
\(3\text{.}\)
-
\(5052\) is an even number since its last digit is
\(2\) .
-
\(1800\) is an even number since its last digit is
\(0\text{.}\)
-
\(1349\) is an odd number since it ends with
\(9\text{.}\)
Example 1.1.2.
Kirui has
\(35\) cows in his farm and wants to group them equally into
\(2\) pens. Will each pen have an equal number of cows? Explain using even and odd number properties.
Solution.
First we identify whether
\(35\) is even or odd.
Since the last digit is
\(5\text{,}\) this makes
\(35\) is an odd number.
An odd number cannot be divided evenly into equal groups.
The best we can do in this case is to divide the cows into two groups: one with
\(18\) cows and the other
\(17\) cows. This means it’s not possible to split the cows evenly across all pens.
-
Classify the following numbers as even or odd using the given criterion.
-
List all the numbers between
\(8102\) and
\(8130\) and identify odd and even number from the range.
-
Find the sum of the first
\(20\) numbers and determine if the result is odd or even.
-
A grade
\(10\) class has
\(52\) students and their class teacher wanted to group them in pairs. Will each group have an equal number of students? Explain using odd or even properties.
\(\textbf{Further activity}\)
Mutula is organizing a party, and he has
\(35\) party hats. Can Mutula arrange the hats in rows where each row has the same number of hats? What does this tell you about the number
\(35\text{?}\)
\(\textbf{Prime and composite numbers}\)
\(\textbf{A prime number}\) is a number that has only two factors, that is,
\(1\) and itself. Example:
\(2,3,5,7,11,...\)
\(\textbf{A factor}\) of a number is a natural number that divides it exactly with no remainder.
For example,
\(6\) is not a prime number because it has more than two factors:
\(1, 2, 3,\) and
\(6\text{.}\) That is,
\(6 = 1 \times 6\) and
\(6 = 2 \times 3\text{.}\)
To identify if a number is prime, check if the number has two factors:
\(1\) and itself.
\(\textbf{Composite numbers}\) are natural numbers greater than
\(1\) that have more than two factors.
Examples:
\(4(\text{factors}:\, 1,2,4), 6(\text{factors:} \,1,2,3,6), 9(\text{factors:} \,1,3,9)\text{.}\) Hence
\(4,6\) and
\(9\) are composite numbers since they have more than
\(2\) factors.
To identify if a number is composite, check if the number has more than two factors. In other words, if it can be divided exactly by numbers other than 1 and itself, then it is a composite number.
-
\(4\) is composite because
\(4 = 1 \times 4 \) and
\(2 \times 2 \text{.}\)
-
\(9\) is composite because
\(9 = 1 \times 9\) and
\(3 \times3\text{.}\)
-
\(10\) is composite because
\(10 = 1 \times 10\) and
\(2 \times 5\)
\(\textbf{NOTE:}\) \(0\) and
\(1\) are neither prime nor composite.
Every composite number has prime factors. That is, it can be broken down into a product of prime numbers.
This helps reinforce the idea of prime factorization, which is a key property of composite numbers.
-
The only even prime number is
\(2\) .
-
All other even numbers greater than
\(2\) are composite.
-
The smallest composite number is
\(4\text{.}\)
-
Odd composite numbers are odd natural numbers greater than
\(1\) that are not prime (e.g.,
\(9, 15, 21,...)\text{.}\)
Think of prime numbers as building blocks, and composite numbers as being made by combining those blocks.
Example 1.1.3.
Which of the following numbers are prime and which are composite?
Solution.
-
\(1021\) has no factors other than
\(1\) and
\(1021\) itself.
Hence
\(1021\) is a prime number.
-
\(1111 = 11 \times 101\) meaning it is divisible by both
\(11\) and
\(101\text{.}\) it is also divisible by
\(1\) and itself.
Therefore,
\(1111\) is a composite number.
-
\(1999\) cannot be divided by any number other than
\(1\) and
\(1999\) itself.
This means that
\(1999\) is a prime number.
-
\(2000 = 2^4 \times 5^3\) which implies that
\(2\) and
\(5\) are its factors. Also, it is divisible by
\(1\) and itself,
\(20\) and
\(100\text{,}\) \(2\) and
\(1000\text{.}\)
Therefore,
\(2000\) is a composite number
-
\(3011\) has no factors other than
\(1\) and
\(3011\) itself, making it a prime number.
-
\(3500 = 2^2 \times 5^3 \times 7\) meaning
\(3500\) has other factors other than
\(1\) and
\(3500\text{.}\)
Hence
\(3500\) is a composite number.
-
Classify the following numbers as prime or composite.
-
Simplify each of the following expressions and state whether the result is a prime or composite number.
-
\(\displaystyle 1024 \times 5 \div 4\)
-
\(\displaystyle \sqrt{144} \times 3 - 9 +4\)
-
\(\displaystyle \sqrt{64} \times 5\)
-
\(\displaystyle 4^2 \times 2 + 4\)
-
\(\displaystyle 49^2 + 6 \div 7\)
-
\(\displaystyle \sqrt{25} \times 2 - 8\)
-
The number
\(51\) is suspected to be prime. Use divisibility rules or the factorization method to determine whether it is a prime or composite number.
-
A teacher writes a two-digit number on the board. The number is prime and ends with
\(3\text{.}\) List all possible numbers it could be.
-
A marathon is divided into
\(42\)-kilometer relay sections. Each runner must cover a distance (in km) that is a composite number. List three possible distances a runner could cover.
-
A class of students forms a rectangular grid. The total number of students is
\(273\text{.}\) Determine whether this number is prime or composite and explain your reasoning.
-
If a number is divisible by
\(2\) and
\(3\text{,}\) what smallest composite number could it be?
Subsection 1.1.2 Classifying real numbers as rational and irrational in different situations
Activity 1.1.2.
-
Working in groups, choose any set of natural numbers between
\(1\) and
\(10\) (e.g.,
\(2, 3, 5,7,..\))
\(\bullet\) Use these numbers to create at least two fractions:
One proper fraction (e.g.,
\(3/5\))
One improper fraction (e.g.,
\(7/4\))
-
Use a calculator to divide each of your fractions.
Write down the decimal value of each.
Example:
\(7 ÷ 4 = 1.75\text{.}\)
-
Choose any set of Natural numbers between
\(1\) and
\(20\text{.}\)
Write each number as a square root.
Example:
\(\sqrt{9}= 3\)(a rational number),
\(\sqrt{2} = 1.414...\)(an irrational number).
-
Classify each number you have created (fractions, decimals, and square roots) as either rational or irrational.
-
What do you notice about the decimal form of rational numbers compared to irrational numbers?
-
Discuss your observations with your fellow learners.
\(\textbf{ Key Takeaway}\)
\(\bullet\) \(\textbf{ Rational number} (\mathbb{Q}):\) A rational number is any number that can be written as a fraction
\(\frac{p}{q}\) where
\(p\) and
\(q\) are integers and
\(q \neq 0\text{.}\)
Example:
\(\frac{2}{3},-3,4 \)
\(\bullet\) \(\textbf{ Irrational number:}\) An irrational number is any number that cannot be expressed as a fraction of two intergers.
Example:
\(\sqrt{7}, \sqrt{2}, \pi\)
\(\bullet\) \(\textbf{Integers}\) consists of positive whole numbers, negative whole numbers and
\(0\text{.}\)
\(\bullet\) The decimal representation of a rational number either terminates (stops at some point) or repeats (continues but has a repeating pattern).
Example:
\(0.375, 3.45454545...\)
\(\bullet\) The decimal representation of an irrational number neither terminates (does not stop) nor repeats (continues without a repeated pattern).
Example:
\(3.14285714..., 4.298103993...\)
\(\bullet\) The square root of a perfect square is a rational number.
Example:
\(\sqrt{16} = 4\) and
\(4\) can be written as
\(\frac{4}{1}\)
\(\bullet\) The square root of an imperfect square is an irrational number.
Example:
\(\sqrt{2} = 1.41421356237\) which is an irrational number.
\(\textbf{ How to determine if a number is rational or irrational.}\)
-
Rule: Check if the number is an integer or a fraction with an integer as the numerator and the denominator. If it is, then it is a rational number.
Example:
\(7\) or
\(\frac{4}{5}\) are both rational numbers because they are either whole numbers or simple fractions.
-
Rule: "If the number is in decimal form, check if the decimal stops at some point. If it stops then the number is a rational number."
Example:
\(3.25\) is rational because the decimal terminates.
-
Rule: If the number is in decimal form, check if the decimal continues. If it continues with a repeated pattern then the number is a rational number and if it continues without a pattern then it is irrational.
Example (rational):
\(0.666… \)(repeating)
xample (irrational):
\(0.1010010001… \)(no pattern)
-
Rule: "If the number is expressed as a square root, find the square root of the number first and identify if it is a perfect or an imperfect square. If it is a perfect square (results to a whole number) then it is rational and if it is an imperfect square, then it is irrational.
Example (rational):
\(\sqrt{49} = 7\)
xample (irrational):
\(\sqrt{2} ≈ 1.414213...\)
Activity 1.1.3.
-
Working in groups, write any
\(5\) numbers between
\(1\) and
\(10\) (e.g.,
\(2, 3, 5,7,..\))
-
Form at least
\(3\) fractions using the numbers you formed above. Form both proper and improper fractions e.g.,
\(\frac{2}{5},\frac{7}{3}\text{.}\)
-
Divide each of the fractions you formed to express it as a decimal. Example:
\(2 \div 5= 0.4, 7 \div 3 =2.\dot{3}\text{.}\)
-
Express the numbers
\(1\) to
\(10\) as square roots. Example:
\(\sqrt{1},\sqrt{2},...,\sqrt{10}\text{.}\)
-
Classify the fractions, decimals, and square root numbers you have formed as rational and irrational numbers.
-
What do you notice about the decimal forms of fractions?
-
Discuss your work with fellow learners.
Example 1.1.4.
Identify if the following numbers are rational or irrational.
-
-
\(\displaystyle \frac{2}{3}\)
-
-
\(\displaystyle \sqrt{20}\)
-
\(\displaystyle \frac{\sqrt{9}}{\sqrt{16}}\)
Solution.
-
Since
\(\pi\) is defined as
\(3.1415926\text{.}\)
We check if the decimal continues.
Hence
\(\pi\) is irrational because its decimal continues without having a repeated pattern.
-
Since
\(\frac{2}{3}\) is a fraction, we check if the fraction consist of integers with the denominator not equal to zero.
Therefore
\(\frac{2}{3}\) is a rational number.
-
To identify if
\(3.75\) is rational or irrational, we check the decimal.
A rational number can have a terminating decimal or a repeating decimal. In this case, the decimal terminates, so the number is rational
-
For
\(\sqrt{20}\text{,}\) first we find its value.
\(\sqrt{20} = 4.472135955\)
\(\sqrt{20}\) has decimal which continues without a repeated pattern.
Hence
\(\sqrt{20}\) is irrational.
-
The value of
\(\frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}\)
\(\frac{3}{4}\) is a fraction with integers on the numerator and the denominator.
Therefore,
\(\frac{\sqrt{9}}{\sqrt{16}}\) is rational.
Example 1.1.5.
Joy is designing a square garden. She measures the total area of the garden to be
\(50\) square meters and wants to find the length of one side. What is the exact length of one side of the garden? Classify the answer as a rational or irrational number.
Solution.
Area of the garden =
\(50 \text{ m}^2\)
To find the length of one side of the square, we take the square root of its area.
Side length =
\(\sqrt{50}\text{.}\)
Simplifying the side length
\(\sqrt{50} = \sqrt{(25 \times 5)} = \sqrt{25} \times \sqrt{2} = 5 \sqrt{2}\text{.}\)
Since
\(\sqrt{2}\) an irrational number, multiplying it by
\(5\) still gives an irrational number.
Therefore, the exact length of one side of the garden is
\(5 \sqrt{2}\) meters, which is an irrational number.
1. Classify the following numbers as rational or irrational giving reasons.
-
\(\displaystyle \sqrt{25}\)
-
-
\(\displaystyle \sqrt{2}\)
-
\(\displaystyle \frac{7}{3}\)
-
-
\(\displaystyle 0.121221222\)
-
-
\(\displaystyle \sqrt{2} + \sqrt{8}\)
-
\(\displaystyle \pi - 3\)
-
\(\displaystyle \frac{\sqrt{4}}{\sqrt{9}} \times 4\)
-
\(\displaystyle 2 \times \sqrt{2}\)
2. A square garden has a perimeter of
\(8\) units. Find its area and identify if it is a rational or irrational number.
3. For each of the following values of
\(m\) state whether
\(\frac{m}{16}\) is rational or irrational.
-
-
-
\(\displaystyle \sqrt{2}\)
-
\(\displaystyle \sqrt{25}\)
-
4. A car is moving at
\(\sqrt{225}\) km/h. Is the speed rational or irrational? Explain your answer.
5. Iregi a grade
\(10\) student measures a triangular shelf in their home and found out its sides of length was
\(\sqrt{12}\) meters,
\(\sqrt{27}\) meters and
\(5\) meters. He wants to find the perimeter of the triangle and identify if it is rational or irrational. Help Iregi to find out if the perimeter is rational or irrational explaining your workings.
6. A rectangular garden has a length of
\(4\) meters and a width of
\(\sqrt{8}\) meters. Find the area of the garden and identify if it is rational or irrational.
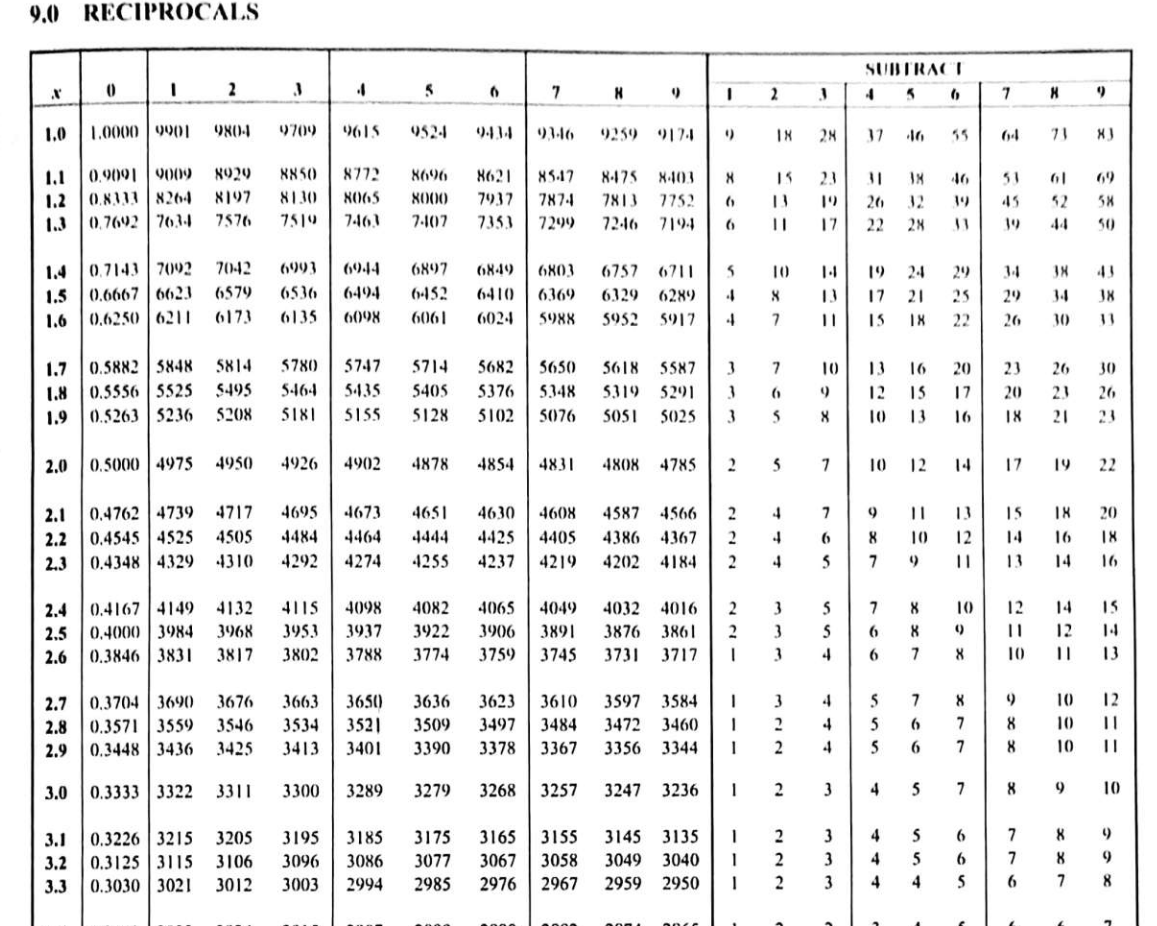
Subsection 1.1.6 Real-world applications of reciprocals of real numbers
Reciprocals are important in various fields, including finance, science, engineering, medicine, and transportation . In disciplines such as physics, chemistry, and manufacturing, dividing rational numbers using reciprocals helps solve real-world problems, from calculating speed and time to determining chemical concentrations and optimizing production efficiency.
In this section, we will explore real-world applications of reciprocals and how they make mathematical computations easier and more practical.
Activity 1.1.8.
Nkirote is a baker and is preparing large orders of bread for a grade
\(10\) student’s event. Each batch of bread requires
\(\frac{2}{3}\) kg of flour, and she has a total of
\(12\) kg of flour. She needs to determine how many full batches she can make. As she prepares, she realizes that each batch also requires
\(\frac{3}{4}\) liters of milk. If she has
\(9\) liters of milk available, she must check whether she has enough for all the batches. To ensure efficiency, she calculates how many full loaves of bread she can produce if each batch yields
\(\frac{2}{5}\) of a loaf per kilogram of flour used.
1. Working in groups, use reciprocals to determine how many full batches of bread the baker can make with
\(12\) kg of flour.
2. Calculate whether
\(9\) liters of milk is enough for all the batches.
3. If each batch produces
\(\frac{2}{5}\) of a loaf per kilogram of flour, how many full loaves can she make?
4. How was reciprocal helpful in dividing quntities while baking?
5. Discuss areas where reciprocals are applied in the real word.
6. Discuss your work with fellow learners.
\(\textbf{Key Takeaway}\)
Here are practical examples of how reciprocals are applied to solve real-world problems:
1. A printing machine can print
\(\frac{5}{6}\) of a book page per second. How long will it take to print
\(20\) pages?
If
\(1\) second =
\(\frac{5}{6}\) of a page, then for
\(20\) pages, we calculate as follows:
\begin{align*}
\text{ Time } =\amp 20 \div \frac{5}{6}\\
=\amp 20 \times \frac{6}{5}
\end{align*}
Multiplying and simplifying we have: Time =
\(\frac{120}{5} = 24\) seconds.
Thus, the printing machines will take
\(24\) seconds to print
\(20\) pages.
2. If a car travels at
\(80\) km/h, to find out the time taken per km we can use reciprocal.
Time per km =
\(\frac{1}{80}\) hours per km.
3. If a factory produces
\(300\) items in
\(5\) hours, then the production rate per hour is:
\(\frac{300}{5} = 60\) items per hour.
To determine how much time is needed per item, we use reciprocal:
Hence, the factory produces
\(1\) item every
\(\frac{1}{60}\) hours.
Example 1.1.12.
Okoth runs
\(3 \frac{1}{4}\) miles in
\(\frac{1}{2}\) an hour. What is her speed in miles per hour?
Solution.
To find speed we divide distance by time such that: speed =
\(\frac{\text{ distance}}{\text{ time}}\text{.}\)
First, we need to convert the fraction
\(3\frac{1}{4}\) into an improper fraction which is
\(\frac{13}{4}\)
Hence, speed =
\(3\frac{1}{4} \div \frac{1}{2} = \frac{13}{4} \div \frac{1}{2}\)
Multiply
\(\frac{13}{4}\) by the reciprocal of
\(\frac{1}{2}\text{.}\)
\(\frac{13}{4} \times \frac{2}{1} = \frac{26}{4}\)
Simplifying
\(\frac{26}{4}\) we get
\(\frac{13}{2}\) which is
\(= 6 \frac{1}{2}\text{.}\)
1. A paint manufacturer claims that
\(1\) liter of paint covers
\(48\) square feet. A customer buys a
\(0.5\)-liter sample and uses it to paint a
\(2\)-foot by
\(4\)-foot section of a wall. To determine whether the sample meets the manufacturer’s claim, first calculate the area it covers. Then, using reciprocals, find how many times
\(0.5\) liters fits into
\(1\) liter. Compare the result with the stated
\(48\) square feet per liter to determine if the sample performs as expected.
2. A gardener can plant
\(\frac{7}{9}\) of a flowerbed per hour. How long will it take to complete
\(18\) flowerbeds?
3. A printer in a publishing company prints
\(\frac{2}{5}\)of a book page per second. How long will it take to print
\(90\) pages at this rate?
4. A car consumes
\(\frac{2}{7}\)of a gallon of fuel per mile. If the fuel tank holds
\(21\) gallons, how many miles can the car travel before running out of fuel?
5. A construction crew is tasked with laying concrete on a road section. A
\(7\) -ton cement truck can produce enough concrete to cover
\(280\) square meters. However, due to supply limitations, only
\(4.5\) tons of cement is available. Using reciprocals, determine how many square meters can be covered with
\(4.5\) tons of cement.
6. A laboratory is preparing a specialized chemical solution. The standard formula states that
\(5 \) liters of a concentrated acid can be diluted to produce
\(150\) liters of usable solution. If the lab technician only has
\(3.75\) liters of the concentrate, use reciprocals to calculate how many liters of usable solution can be prepared.
7. A group of workers can complete
\(\frac{3}{4}\) of a construction task in
\(6\) hours. How much time will it take to finish the entire task at the same rate?