Skip to main content

Grade 10 Mathematics: Learners’ Book

INNODEMS

Section 2.4 Trigonometry 1

By the end of this topic, you should be able to:
  1. Define and apply trigonometric ratios (sine, cosine, tangent).
  2. Use the Pythagorean Theorem to find missing sides in right-angled triangles.
  3. Solve for unknown sides and angles using trigonometric ratios.
  4. Apply trigonometric values of special angles (\(30^\circ, \,45^\circ, \,60^\circ\)) in solving geometric problems.
  5. Analyze and interpret relationships between angles and side lengths in various contexts to solve application problems.

Subsection 2.4.1 Trigonometric Ratios of Acute Angles

Subsubsection 2.4.1.1 Tangent of an Acute Angle

Activity 2.4.1.
\(\textbf{Work in pairs}\)
What you require:
  • A piece of paper
  • A ruler
  • A pencil
  1. Using a piece of paper, a ruler, and a pencil, carefully draw the diagram shown below.
    Figure 2.4.1. fig 1.2
  2. Measure and record the lengths of \(OB,\,BQ,\,OC,\,CR,\,OA,\, \text{and}\,AP\)using a ruler..
  3. Identify whether triangles \(OPA,\,OQB,\,\text{and}\,ORC\) are similar.
    If they are similar, compare the ratios of their corresponding sides.
  4. Calculate the following ratios:
    \(\frac{PA}{OA}\)
    \(\frac{QB}{OB}\)
    \(\frac{RC}{OC}\)
  5. Observe the ratios from the previous step.
    What do you notice about the relationship between them?
  6. Considering the parallel lines \(BQ\text{,}\) \(AP\) and \(RC\) examine the relationship between the vertical and horizontal distances.
    What do you notice about their ratios?
  7. Use a protractor to measure the angle marked \(x^\circ\) in the diagram.
  8. Share your observations and conclusions with your classmates.
\(\textbf{Extended Activity}\)
  1. The inclination of the observer’s line of sight to the top of a \(10\,m\) high flag pole, positioned \(15\,m\) away, can be determined using a scale drawing, as illustrated in the diagram below.
    Figure 2.4.2.
    What do we call the angle represented by \(x\text{?}\)
  2. Look at the triangle shown in \(\textbf{Figure 2.4.3.}\)
    Express \(tan\,\alpha\) in terms of the lengths of the sides of the triangle.
    Hint: Recall that in a right-angled triangle:
    \begin{equation*} tan\, \alpha=\frac{\text{opposite side​}}{\text{adjacent side}} \end{equation*}
\(\textbf{Key Takeaway}\)
When given the triangle below, you will notice the following:
Figure 2.4.3.
  1. The triangles \(OPA,\,OQB,\,\text{and }\, ORC\) are similar.
    This means that the ratios of their corresponding sides are equal:
    \begin{equation*} \frac{PA}{OA}=\frac{QB}{OB}=\frac{RC}{OC}=\frac{15}{10}=1.5 \end{equation*}
  2. For any line parallel to \(BQ\text{,}\) rthe ratio of vertical distance to horizontal distance remains the same in each triangle. In this case, the ratio is\(1.5\text{.}\)
    This constant ratio, \(\frac{\text{Vertical distance}}{\text{Horizontal distance}}\) is called the \(\textbf{tangent of angle} \, VOT\text{.}\)
    Therefore, the tangent of \(x^\circ\) is \(1.5\) which can be written as:
    \begin{equation*} \text{tan}\,x^\circ=1.5 \end{equation*}
    The tangent of an angle depends only on the size of the angle, not on the triangle’s size.
The diagram below shows a right-angled triangle \(ABC\text{,}\) where:
\begin{equation*} \angle ABC = \theta\text{.} \end{equation*}
Figure 2.4.4.
  • The side \(AC\) is the vertical side, which is \(\textbf{opposite}\) to angle \(\theta\text{.}\)
  • The side \(AB\) is the horizontal side, which is \(\textbf{adjacent}\) to angle \(\theta\)
  • The side \(BC\) is the \(\textbf{hypotenuse}\text{,}\) which is the longest side of the right-angled triangle.
In this case, the tangent of angle \(\theta\) is defined as the ratio of the opposite side to the adjacent side:
\begin{equation*} \text{tan}\,\theta = \frac{\textbf{Opposite side}}{\textbf{Adjacent side}}= \frac{AC}{AB}\text{.} \end{equation*}
Example 2.4.5.
Find the tangent of the indicated angles using the given measurements below.
Solution.
The above diagram the sides given are,
Opposite side \(=3\,cm\)
Adjacent side \(= 4\,cm\)
Therefore,
\begin{align*} \text{tan} \, \theta = \amp \frac{\text{Opposite }}{\text{Adjacent }} \\ =\amp \frac{3\,cm}{4\,cm} \\ = \amp \frac{3}{4}\\ =\amp 0.75 \end{align*}
Therefore, \(\text{tan} \,\theta=0.75\)
Example 2.4.6.
Find the tangent in the indicated angle below.
Solution.
The first thing you should do is to calculate the perpendicular height of the Triangle then identify the opposite and the adjacent sides of angle \(\theta\) and angle \(\alpha\text{.}\) Finaly find there tangents.
Finding the perpendicular height.
We use pythagorean relationship that is
\begin{equation*} H^2=b^2+h^2 \end{equation*}
\begin{align*} h^2=\amp H^2-b^2 \\ =\amp 5^2=3^2\\ =\amp 25-9 \\ =\amp 16 \\ \sqrt{h^2}= \amp \sqrt{16} \\ h= \amp 4\,cm \end{align*}
Finding \(\text{tan} \theta\)
\(\text{tan} \, \theta = \frac{\text{Opposite }}{\text{Adjacent }}\)
The opposite side \(=3\,cm\)
The adjacent side \(=4\,cm\)
\begin{align*} \text{tan} \, \theta= \amp \frac{3\,cm}{4\,cm} \\ =\amp \frac{3}{4}\\ =\amp 0.75 \end{align*}
Finding \(\text{tan} \alpha\)
\(\text{tan} \, \alpha = \frac{\text{Opposite }}{\text{Adjacent }}\)
The opposite side \(=4\,cm\)
The adjacent side \(=3\,cm\)
\begin{align*} \text{tan} \, \theta= \amp \frac{4\,cm}{3\,cm} \\ =\amp \frac{4}{3}\\ =\amp 1.3333333333\\ = \amp 1\frac{1}{3} \end{align*}
Therefore,
\begin{align*} \text{tan} \, \theta= \amp 0.75\\ \text{tan} \, \alpha=\amp 1.333 \end{align*}
\({\color{black} \textbf{Tables of Tangents}}\)
Activity 2.4.2.
\(\textbf{Work in groups}\)
What you require: Printed Table of Tangent, a \(30\,cm\) ruler, pencil, and calculator (for verification).
  1. What is the tangent of an angle?
  2. How do we use a Table of Tangents?
  3. Use your Table of Tangent to find the folowing tangents.
    1. \(\displaystyle 42^\circ\)
    2. \(\displaystyle 35^\circ\)
    3. \(\displaystyle 90^\circ\)
    4. \(\displaystyle 42^\circ \, 47^′\)
  4. Discuss your findings with other groups in your class.
\(\textbf{Key Takeaway}\)
Special tables have been prepared and can be used to obtain tangents of acute angle (see tables of natural tangents in your mathematical tables). The technique of reading tables of tangents is similar to that of reading tables of logarithms or square roots.
Here’s how you can use it:
  1. Identify the angle
    • Find the given angle in the leftmost column (if degrees) or the top row (if radians).
  2. Locate the Tangent Value
    • Read across the row (or down the column) to find the corresponding tangent value.
Note
  1. In the tables of tangents, the angles are expressed in decimals and degrees or in degrees and minutes.
  2. One degree is equal to \(60^′ \, (60\, \text{minutes})\) . Thus, \(30^′ = 0.50^\circ, \,54^′ = 0.9^\circ\, \text{and} \,6^′= 0.1^\circ.\text{.}\)
From the table, the values of tangents increase as the angles approach \(90^\circ\)
Example 2.4.7.
Find the tangent of each of the following angles from the table:
  1. \(\displaystyle 60^\circ\)
  2. \(\displaystyle 52^\circ\)
  3. \(\displaystyle 46.7^\circ\)
  4. \(\displaystyle 52^\circ \, 47^′\)
Solution.
  1. Find \(tan(60^\circ)\)
    Locate \(60^\circ \)in the table.
    Read the corresponding tangent value. that is
    \begin{equation*} tan(60^\circ)=1.732 \end{equation*}
  2. Find \(tan(52^\circ)\)
    Locate \(52^\circ\) in the table.
    Read the corresponding tangent value. that is
    \begin{equation*} tan(52^\circ)=1.279 \end{equation*}
  3. Find \(tan(46.7^\circ)\)
    Locate \(46.7^\circ\) in the table.
    Read the corresponding tangent value. that is
    \begin{equation*} tan(46.7^\circ)=1.0612 \end{equation*}
  4. Find \(tan(52^\circ \, 47^′)\)
    Convert \(47^′\) to degrees by deviding by \(60\)
    \begin{align*} (\frac{47}{60})^\circ =\amp 0.78^\circ \end{align*}
    Therefore,
    \begin{equation*} tan\,52^\circ \, 47^′= 52.78^\circ \end{equation*}
    Using decimal tables, \(tan\, 52.7^\circ = 1.3127 \text{.}\) From the difference column under \(8\) reads \(0.0038\)
    Therefore,
    \begin{align*} tan\,52^\circ \, 47^′=\amp 52.78^\circ \\ =\amp 1.3127+ 0.0038\\ =\amp 1.3165 \end{align*}
Example 2.4.8.
Using natural tangents in your mathematical tables, find \(\alpha\) as shown in the figure below.
Solution.
Opposite \(=4\,cm\)
Adjacent \(=3\,cm\)
\begin{align*} Tan \, \alpha =\amp \frac{\text{Opposite}}{\text{Adjacent}} \\ = \amp \frac{4\,cm}{3\,cm} \\ = \amp 1.3333 \end{align*}
Note that \(1.3333\) cannot be read directly from the tables of tangents. Therefore, look for a number nearest to \(1.3333\) from the tables. In this case, the nearest number is \(1.3319\) The angle whose tangent is \(1.3319\) is \(53.1^\circ\)
The difference between \(1.3333\) and \(1.3319\) is \(14.\text{.}\) From the difference column in the tangent tables, the nearest number to \(14.\) is \(9\) which gives a difference of \(0.44\text{.}\)
Adding \(0.44\) to \(53.1^\circ\) we get \(53.54^\circ\text{.}\)
Therefore, the angle whose tangent is \(1.3333\) \(=53.54^\circ\)
Thus, \(\alpha=53.54^\circ\text{.}\)
\(\textbf{Exercises}\)
  1. Read from tables the tangent of:
    1. \(\displaystyle 88^\circ\,46^′\)
    2. \(\displaystyle 60^\circ\,46^′\)
    3. \(\displaystyle 45^\circ\)
  2. Express each of the following in degrees and minutes:
    1. \(\displaystyle 26.75^\circ\)
    2. \(\displaystyle 40\frac{1}{2}^\circ\)
    3. \(\displaystyle 56\frac{1}{4}^\circ\)
  3. Use Natural logarithm of tangents to find the length \(PR\) in the figure below. (leave your answer to \(2\, \textbf{decimal places}\))
  4. A ladder leans against a wall so that its foot is \(4.5 \,m\) away from the foot of the wall and its top is \(10\,\) up the wall. Calculate the angle it makes with the ground .
  5. In a right-angled triangle, the shorter sides are \(6.5\, cm\) and \(12.2 \,cm\) long. Find the sizes of its acute angles.

Subsubsection 2.4.1.2 Sine and Cosine of an Acute Angle

Activity 2.4.3.
\(\textbf{Work in groups}\)
What you require; A piece of paper, a ruler and a pencil.
  1. The figure below shows \(AP,\,BQ, \textbf{and}\,CR\) perpendicular to \(OV \text{and } \, \angle \, TOV=\theta \)
    Figure 2.4.9. fig 1.5
  2. Copy the above figure in your writing materials.
    Measure lengths \(OA,\,OP,\,AP,\,OQ,\,OB,\,BQ,\,OR,\,OC \,\text{and}\,CR \)
  3. Fill in the following;
    1. \(\frac{AP}{OP}=\)____
    2. \(\frac{BQ}{OQ}=\)____
    3. \(\frac{CR}{OR}=\)____
  4. What do you notice about the ratios of roman (i...iii).
  5. Fill also the following;
    1. \(\frac{OA}{OP}=\)____
    2. \(\frac{OB}{OQ}=\)____
    3. \(\frac{OC}{OR}=\)____
  6. What do you notice about these ratios (5) above.
  7. Discuss your findings with other groups in your class.
\(\textbf{Key Takeaway}\)
You will notice that,
  1. The ratios of (3) are the same and is expressed as;
    \(\frac{AP}{OP}=\frac{BQ}{OQ}=\frac{CR}{OR}\)
    This constant value is obtained by taking the ratio of the side opposite to the angle \(\theta \) to the hypotenuse side in each case. This ratio is called the sine of angle \(\theta \text{,}\) which can be written as as \(sin \, \theta\text{.}\)
  2. The ratios of (5) are the same and is expressed as;
    \(\frac{OA}{OP}=\frac{OB}{OQ}=\frac{OC}{OR}\)
    This constant value is obtained by taking the ratio of the side adjacent to the angle \(\theta \) to the hypotenuse side in each case. This ratio is called the cosine of angle \(\theta \text{,}\) which can be written as \(cos \, \theta\text{.}\)
In general, given a right-angled triangle whith \(\textbf{opposite side, adjacent side}\) and \(\textbf{hypotenuse side}\) as shown,
\begin{align*} tan \, \theta=\amp \frac{\text{Opposite}}{\text{Adjacent}} \\ cos\, \theta =\amp \frac{\text{Adjacent}}{\text{Hypotenuse}}\\ sin\,\theta =\amp \frac{\text{Opposite}}{\text{Hypotenuse}} \end{align*}
\(\textbf{The above formula also applies to the trigonometric ratios for}\) \(\alpha\text{.}\)
Example 2.4.10.
In the figure below, \(MN=5\, cm\,,NO=12\,cm \,\text{and} \, \angle MNO=90^\circ\text{.}\) Calculate:
  1. \(\displaystyle sin\,\theta\)
  2. \(\displaystyle cos\,\theta\)
Solution.
  1. \begin{align*} sin\,\theta=\amp \frac{\text{opposite}}{\text{hypotenuse}}\\ =\amp \frac{MN}{MO}\\ =\amp \frac{5}{MO} \end{align*}
    Recall:
    \begin{align*} MO^2=\amp 12^2+5^2 \\ =\amp 144+ 25\\ =\amp 169\\ MO= \amp 13\,cm \end{align*}
    Thus,
    \begin{align*} sin \,\theta= \amp \frac{5}{13}\\ =\amp 0.3846 \end{align*}
  2. \begin{align*} cos\,\theta=\amp \frac{\text{adjacent}}{\text{hypotenuse}}\\ =\amp \frac{NO}{MO} \\ =\amp \frac{12}{13} \\ = \amp 0.9231 \end{align*}
Example 2.4.11.
A ladder leans against a wall, forming a \(70^\circ\) angle with the ground. If the ladder is \(5\) meters long, how high does it reach on the wall?
Solution.
Using \(sin⁡\text{,}\) since we need the opposite side:
\begin{align*} sin\, 70^\circ=\amp \frac{\text{height}}{\text{hypotenuse}}\\ 0.9397=\amp \frac{\text{height}}{5}\\ \text{height}=\amp 5 \times 0.9397 \\ =\amp 4.6985 \,m \end{align*}
The ladder reaches \(4.6985 \,m\) up the wall.
\(\textbf{Exercises.}\)
  1. In the figure given below,
    Find;
    1. \(\displaystyle sin\,\alpha\)
    2. \(\displaystyle cos\,\alpha\)
  2. A flagpole \(12\) meters tall casts a shadow of \(8\) meters on the ground.
    1. What is the angle of elevation of the sun?
    2. If the shadow increases to \(10\) meters, what will be the new angle of elevation?
  3. An airplane takes off at an angle of \(18^\circ\) to the ground. After flying \(500\) meters,
    1. How high is the airplane above the ground?
    2. How far has it traveled horizontally from the starting point?
  4. A ladder \(5\) meters long leans against a vertical wall, making an angle of \(65^\circ\) with the ground as shown.
    1. How high does the ladder reach on the wall?
    2. How far is the base of the ladder from the wall?
\({\color{black} \textbf{Tables of Sines and Cosines}}\)
Activity 2.4.4.
\(\textbf{Work in groups}\)
What you require: A scientific calculator{for verification}, ruler and pencil, a printed table of sine and cosine values.
  1. Complete the Trigonometric Table.
    Fill in the missing values in the table below. Use a calculator to check your answers if needed.
    Angle(\({\color{black}^\circ}\)) \({\color{black} sin\,\theta}\) \({\color{black} cos\,\theta}\) \({\color{black} sin(90^\circ-\theta)}\) \({\color{black}cos(90^\circ-\theta)}\)
    \(0^\circ\) \(0.0000\) \(1.0000\)
    \(30^\circ\) \(0.5000\) \(1.0000\)
    \(45^\circ\)
    \(60^\circ\)
    \(45^\circ\) \(1.0000\) \(0.0000\)
  2. Analyze the following.
    • Compare \(sin\,\theta\) with \(cos(90^\circ-\theta)\text{.}\) What do you notice?
    • Compare \(sin\,\theta\) with \(cos(90^\circ-\theta)\text{.}\) What pattern do you see?
  3. Discuss your work with other groups in class.
\(\textbf{Extended Activity}\)
Activity 2.4.5.
\(\textbf{Work in groups}\)
What you require: Ruler, pencil, graph paper and a protractor.
  1. Draw a right triangle and label the opposite, adjacent and hypotenuse on all three sides and indicate the angle \(\theta\text{.}\)
  2. Measure both the length(\(cm\)) and angle \(\theta\text{.}\)
  3. Find \(sin(\theta),\,cos(\theta)\, \text{and}\, tan\,\theta \text{.}\)
  4. Divide \(sin(\theta) \,\text{by}\, cos(\theta)\) and record your answers on the table below.
    Side Measurement Length (\(cm\)) Ratio calculation Results
    Opposite \(sin(\theta)= \frac{\text{Opposite}}{\text{Hypotenuse}}\)
    Adjacent \(cos(\theta)= \frac{\text{Adjacent}}{\text{Hypotenuse}}\)
    Hypotenuse \(tan(\theta)= \frac{\text{Opposite}}{\text{Adjacent}}\)
  5. Repeat the procedure with a different right triangle.
  6. How are \(sin\,\theta,\, cos\,\theta,\, \text{and}\,tan\, \theta \) related?
  7. Discuss your work with other learners.
\(\textbf{Key Takeaway}\)
When you look at the tables of Cosine and sine, you will notice that,
  1. The values of their sines increase from \(0\) to \(1\text{.}\)
  2. The values of their cosines decrease from \(1\) to \(0\)
Therefore, the values in the difference column of cosine tables have to be subtracted and those in the difference columns of the sine tables have to be added.
Generally,
The values of sine and cosine ranges from \(0\) to \(1\)(\(0\leq \theta \leq 1\)).
As the angles increase from \(0^\circ\) to \(90^\circ\text{:}\)
Example 2.4.12.
Read the sine and cosine values of the following angles from the tables.
  1. \(\displaystyle 46^\circ\)
  2. \(\displaystyle 45.5^\circ\)
  3. \(\displaystyle 75.67^\circ\)
Solution.
  1. \(sin\,46^\circ\)
    Locate \(46^\circ\)in the sine and cosine table.
    Read the corresponding sine value. That is
    \begin{equation*} sin\,46^\circ= 0.7193\text{,} \end{equation*}
    \(cos\,46^\circ\)
    Read the corresponding cosine value. That is
    \begin{equation*} cos\,46^\circ= 0.6947\text{,} \end{equation*}
  2. \(sin\,45.5^\circ\)
    Locate \(45.5^\circ\)in the sine and cosine table.
    Read the corresponding sine value. That is
    \begin{equation*} sin\,45.5^\circ= 0.7133\text{,} \end{equation*}
    \(cos\,45.5^\circ\)
    Read the corresponding cosine value. That is
    \begin{equation*} cos\,45.5^\circ= 0.7009\text{,} \end{equation*}
  3. \(sin\,75.67^\circ\)
    Using decimal tables, \(sin\,75.6^\circ=0.9686\text{.}\) From the difference column under \(7\) reads \(0.0003\)
    Therefore,
    \begin{align*} sin\,75.67^\circ=\amp 0.9686+0.0003\\ = \amp 0.9689 \end{align*}
    \(cos\,75.67^\circ\)
    Using decimal tables, \(cos\,75.6^\circ=0.2487\text{.}\) From the difference column under \(7\) reads \(0.0012\)
    Therefore,
    \begin{align*} cos\,75.67^\circ=\amp 0.2487-0.0012\\ = \amp 0.2475 \end{align*}
Example 2.4.13.
Find the value of \(t\) and \(w\) in the figure shown below (Using sine and cosine tables).
Solution.
Recall that;
\(sin\,\theta=\frac{\text{opposite}}{\text{Hypotenuse}}=\frac{\text{t}}{8}\)
\(cos\,\theta=\frac{\text{opposite}}{\text{Hypotenuse}}=\frac{\text{w}}{8}\)
Therefore,
\begin{align*} sin\,54.7^\circ=\amp \frac{\text{t}}{8}\\ 8\,sin\,54.7^\circ=\amp \text{t} \end{align*}
But, from tables of sine, \(sin\,54.7^\circ=0.8161\)
Therefore,
\begin{align*} \text{t} =\amp 8 \times 0.8161 \\ =\amp 6.5288 \end{align*}
\begin{align*} cos\,54.7^\circ=\amp \frac{\text{w}}{8}\\ 8\,cos\,54.7^\circ=\amp \text{w} \end{align*}
But, from tables of cosine, \(cos\,54.7^\circ=0.5779\)
Therefore,
\begin{align*} \text{w} =\amp 8 \times 0.5779 \\ =\amp 4.6232 \end{align*}
\(\textbf{Exercises}\)
  1. Find from tables the angle whose sine and cosine is:
    1. \(\displaystyle 0.4467\)
    2. \(\displaystyle 0.5875\)
    3. \(\displaystyle 0.0004\)
  2. Read from the tables the sine and the cosine of:
    1. \(\displaystyle 45.46^\circ\)
    2. \(\displaystyle 52^\circ\, 9^′\)
    3. \(\displaystyle 25^\circ\, 45^′\)
  3. The figure below shows an isosceles triangle in which \(AB = AC = 9\, cm\text{.}\) Angle \(BAC\) is \(100^\circ\text{.}\) Calculate the length of BC.

Subsection 2.4.2 Sines and Cosines of Complimentary Angles

Activity 2.4.6.

\(\textbf{Work in pairs}\)
What you require: A pencil, a ruler, a sciantific calculator (\(\textbf{for verification}\)), working material and a printed sine and cosine table.
  1. Read from the tables the values of the following pairs of angles.
    1. \(\displaystyle sin\,40^\circ \quad cos\,50^\circ\)
    2. \(\displaystyle cos\,30^\circ \quad sin\,60^\circ\)
    3. \(\displaystyle sin\,70^\circ \quad cos\,20^\circ\)
    4. \(\displaystyle sin\,80^\circ \quad cos\,90^\circ\)
  2. What do you notice on the results obtained in "1"?
  3. Discuss your work with other learners in your class.
\(\textbf{Complementary angles}\) are two angles whose sum is \(90^\circ\) (or \(\frac{\pi}{2}\)radians). The sine and cosine functions of complementary angles have a special relationship:
\begin{align*} sin(90^\circ-\theta)=\amp cos \, \theta \\ cos(90^\circ-\theta)=\amp sin\, \theta \end{align*}
For example, if \(y\) is one angle and \(x\) is the other angle, then:
\begin{align*} y+x =\amp 90^\circ \end{align*}
Generally,For any two complementary angles \(x \) and \(y\text{,}\) the following relationships hold:
\(sin\,x=cos\,y\) and \(cos\,x=sin\,y\text{.}\)
This means that the sine of one angle is equal to the cosine of the other and vice versa.

Example 2.4.14.

Find acute angles \(\theta\) and \(\beta\) if:
  1. \(cos\,45^\circ=sin\,\alpha\text{.}\)
  2. \(cos\,\beta=sin\,5\beta\text{.}\)
  3. \(sin\,2\alpha=cos\,30^\circ\text{.}\)

Solution.

  1. \(cos\,45^\circ=sin\,\alpha\text{.}\)
    Implies that,
    \begin{align*} 45^\circ+\alpha=\amp 90^\circ \\ =\amp 90^\circ -45^\circ\\ =\amp 45^\circ \end{align*}
  2. \(cos\,\beta=sin\,5\beta\text{.}\)
    Implies that,
    \begin{align*} \beta+5\beta=\amp 90^\circ \\ 6\beta=\amp 90^\circ \\ \beta=\amp\frac{90^\circ}{6} \\ = \amp 15^\circ \end{align*}
  3. \(sin\,2\alpha=cos\,30^\circ\text{.}\)
    Implies that,
    \begin{align*} 2\alpha+30^\circ=\amp 90^\circ \\ 2\alpha=\amp 90^\circ-30^\circ \\ \alpha=\amp \frac{60^\circ}{2} \\ = \amp 30^\circ \end{align*}

Example 2.4.15.

\(A\) and \(B\) are complementary angles.If \(A=\frac{1}{2}B\text{,}\) find:
  1. \(\displaystyle sin\,A\)
  2. \(\displaystyle cos\,A\)

Solution.

When we say \(A \,\text{and} \,B\) are complimentary it implies that, \(A+B=90^\circ\)
Also we have, \(A=\frac{1}{2}B\)
First, Write \(A\) interms of \(A\) that is,
\begin{align*} A= \amp \frac{1}{2}B\\ B= \amp 2A \end{align*}
Since, \(A+B=90^\circ\text{,}\) subtitute \(B=2A\)
\begin{align*} A+2A=\amp 90^\circ\\ 3A=\amp 90^\circ\\ A= \amp \frac{90^\circ}{3}\\ =\amp 30^\circ \end{align*}
Therefore,
  1. \begin{align*} sin\,A=\amp sin\,30^\circ \end{align*}
    Use tables of sine to find \(sin\,30^\circ\)
    \(sin\,30^\circ=0.5000\)
    Therefore, \(sin\,A=0.5000\)
  2. \begin{align*} cos\,A=\amp cos\,30^\circ \end{align*}
    Use tables of cosine to find \(cos\,30^\circ\)
    \(cos \,30^\circ=0.8660\)
    Therefore, \(cos\,A=0.8660\)
\(\textbf{Exercises}\)
  1. If \(\theta\) is an acute angle such that \(sin\,(\theta)=\frac{3}{5}\text{,}\) find \(cos(90^\circ-\theta)\text{.}\)
  2. In the right-angled triangle below, find \(sin\, \theta \) and \(cos \,\theta\text{,}\) then verify that \(sin \,\theta= cos\, \theta\text{.}\)
  3. Given that \(cos(32^\circ) = 0.848\text{,}\) find the value of \(sin(58^\circ)\) without using a calculator.
  4. A ladder leans against a wall, making a \(65^\circ\) angle with the ground. Find the height at which the ladder touches the wall if the ladder is \(10\,m\) long.

Subsection 2.4.3 Trigonometric ratios of Special Angles((30°, 45° and 60°))

Subsubsection 2.4.3.1 Tangent, Cosine and Sine of 45°

In this section you will use isosceles right-angle triangle to explore on how to find Tangent, Cosine and Sine of \(45^\circ\)
An isosceles triangle is a triangle whose two sides and base angles are equal.
Activity 2.4.7.
\(\textbf{Work in groups}\)
What you require: A ruler, a piece of paper and a protractor.
  1. Draw the isosceles right-angle triangle like the one below,(ensure that two sides are equal)
  2. Measure the angle that substend the Hypotenues and the adjacent that is \(\theta\text{.}\)
  3. Measure the length \(PQ \, \text{and}\, QR\)
    What do you notice about \(PQ \, \text{and}\, QR\)
  4. Find the following trigonometrc ratios:
    1. \(\displaystyle tan \, \theta\)
    2. \(\displaystyle cos \, \theta\)
    3. \(\displaystyle sin \, \theta\)
  5. Compare the value of \(cos \, \theta \, \text{and} \,sin \, \theta \text{,}\) How do they relate?
\(\textbf{Key Takeaway}\)
Look at the figure below;
To find the tangent, cosine and sine of \(45^\circ\text{,}\) find first the length \(PR\)
\begin{align*} PR^2=\amp 1^2+1^2 \\ = \amp 1+1 \\ =\amp 2\\ PR=\amp \sqrt{2} \end{align*}
Therefore,
\begin{align*} Sin\,45^\circ=\amp \frac{1}{\sqrt{2}} \\ Cos\,45^\circ=\amp \frac{1}{\sqrt{2}}\\ Tan\,45^\circ=\amp 1 \end{align*}

Subsubsection 2.4.3.2 Tangent, Cosins and Sine of 30° and 60°

In this section, you will be using equilateral triangle to find the Tangent, Cosine and Sine of \(30^\circ \, \text{and}\, 60^\circ\) .
Equilateral triangle is a triangle whose sides and angles are equal.
\(\textbf{Work at home}\)
Use the same procidure above to identify the Tangent, Cosine and Sine of \(30^\circ \, \text{and}\, 60^\circ\) using equilateral triangle.
Discuss your work with other learners in your class.
\(\textbf{Further activity}\)
Activity 2.4.8.
\(\textbf{Work in groups}\)
What you require: Ruler, pencil, protractor, graph paper.
  1. Drawing a \(45-45-90\text{:}\)
    1. Draw a square.
    2. Draw a diagonal to make two triangles.
    3. Label angles (\(45^\circ, \,45^\circ,\, 90^\circ\)).
  2. Draw \(30-60-90\text{:}\)
    1. Draw an equilateral triangle.
    2. Draw a line from a corner to the middle of the opposite side.
    3. Label angles (\(30^\circ, \,60^\circ,\, 90^\circ\)).
  3. Measure and Calculate:
    • Measure sides of each triangle.
    • Calculate sin, cos, tan for \(30^\circ, 45^\circ, 60^\circ\) angles.
    • Record your results in the table below.
      Angle Triangle type Opposite side length Adjacent side length Hypotenuse length \(sin(\theta)=\frac{\text{Opposite}}{\text{Hypotenuse}}\) \(cos(\theta)=\frac{\text{Adjacent}}{\text{Hypotenuse}}\) \(tan(\theta)=\frac{\text{Opposite}}{\text{Adjacen}}\)
      \({\color{blue} 30^\circ}\) \(30-60-90\)
      \({\color{blue} 60^\circ}\) \(30-60-90\)
      \({\color{blue} 45^\circ}\) \(45-45-90\)
  4. Discuss your result with other . What do you notice for the \(\textbf{Special Angles}\) (\(30^\circ, 45^\circ, 60^\circ\))?
\(\textbf{Essential concepts.}\)
The figure below shows an equilateral triangle \(ABC\text{.}\) \(AD\) Is the perpendicular bisector of \(BC\text{.}\)
Notice that;
length \(AD\) is given by,
\begin{align*} AD^2=\amp 2^2-1^2\\ = \amp 4-1\\ AD= \amp \sqrt{3} \end{align*}
Therefore, \(sin\,30^\circ=\frac{1}{2},\quad cos\,30^\circ=\frac{\sqrt{3}}{2},\quad \text{and} \quad tan\,30^\circ=\frac{1}{\sqrt{3}}\)
Similarly,
\(sin\,60^\circ=\frac{\sqrt{3}}{2},\quad cos\,60^\circ=\frac{1}{2},\quad \text{and} \quad tan\,60^\circ=\sqrt{3}\)
Conclusion
  • Sin and Cos are just swapped between \(30^\circ \) and \(60^\circ \text{.}\)
  • Tan \(30^\circ \) is small while tan \(60^\circ \) is large.
  • \(sin\,\theta \times sin \, \theta \text{,}\) can be written as \(sin^2\,\theta\)
Example 2.4.16.
Simplify the following without using tables or calculator.
  1. \(\displaystyle sin \,30^\circ \, cos\,45^\circ\)
  2. \(\displaystyle 8\,cos\,45^\circ\, sin\,45^\circ \)
  3. \(\displaystyle sin\,60^\circ\, cos\,45^\circ +sin\,30^\circ\,tan\,45^\circ\)
Solution.
  1. \begin{align*} sin \,30^\circ \, cos\,45^\circ= \amp \frac{1}{2} \times \frac{1}{\sqrt{2}} \\ =\amp \frac{1}{2\sqrt{2}} \end{align*}
  2. \begin{align*} 8\,cos\,45^\circ\, sin\,45^\circ=\amp \left( 8\times \frac{1}{\sqrt{2}} \right) \times \frac{1}{\sqrt{2}}\\ =\amp \frac{8}{\sqrt{2}} \times \frac{1}{\sqrt{2}} \\ =\amp \frac{8}{\sqrt{2} \times \sqrt{2}} \\ =\amp \frac{8}{2} \\ = \amp 4 \end{align*}
  3. \begin{align*} sin\,60^\circ\, cos\,45^\circ +sin\,30^\circ\,tan\,45^\circ =\amp \left(\frac{\sqrt{3}}{3} \times \frac{1}{\sqrt{2}}\right) +\left(\frac{1}{2} \times 1 \right)\\ = \amp \frac{\sqrt{3}}{2\sqrt{2}} + \frac{1}{2} \\ =\amp \frac{\sqrt{3}+ \sqrt{2}}{2\sqrt{2}} \end{align*}
Example 2.4.17.
The angle at the vertex of a cone is \(90^\circ\text{.}\) If the slant height is \(3\sqrt{2\,cm}\text{.}\) Find without using tables:
  1. The diameter of the cone
  2. The height of the cone.
Solution.
Since the vertex angle is \(90^\circ\text{,}\) the cone can be thought of as half of a right circular cone, meaning that the base of the cone forms the hypotenuse of a right-angled triangle.
Let:
  • \(r\) be the radius of the base,
  • \(h\) be the height of the cone,
  • \(l=3\sqrt{2\,cm}\) be the slant height (hypotenuse of the right-angled triangle).
Since the triangle formed is a right-angled isosceles triangle (because of the \(90^\circ\) vertex angle), we can say:
\(r=h\)
Since the right-angled triangle has radius \(r\) and height \(h\text{,}\) we use:
\(r^2=h^2=l^2\)
Since \(r=h\text{,}\) we substitute:
\begin{align*} r^2+r^2=\amp \left(3\sqrt{2}\right) \\ 2r^2= \amp 9 \times 2\\ r^2= \amp 18 \\ ^2=\amp 9 \\ r=\amp 3\,cm \end{align*}
  1. The diameter of the cone is:
    Diameter \(=2r=2(3)=6\,cm\)
  2. The height of the cone;
    Since \(h=r\text{,}\) we conclude:
    \(h=3\,cm\)
\(\textbf{Exercises}\)
  1. The angle made by the arms of an upright pair of dividers and the horizontal is \(45^\circ\text{.}\) The vertical distance from the horizontal to the vertex is \(15\,cm\text{.}\) Find without using tables:
    1. The horizontal distance between the tips of the arms.
    2. The length of the arms.
  2. Without using a calculator, find
    \(sin\,60^\circ+cos\,30^\circ\)
  3. Given that \(\theta=45^\circ\text{,}\) calculate:
    \(tan^2\,\theta-sin^2\,\theta\)
  4. Using the triangle below, calculate the value of:
    1. \(\displaystyle sin \,30^\circ\)
    2. \(\displaystyle cos \,60^\circ\)
    3. \(\displaystyle tan \,30^\circ\)
  5. Given: \(sin\,\theta = \frac{1}{2}\)
    Find the angle \(\theta\text{,}\) where \(\theta^\circ \leq \theta \leq 90^\circ\)

Subsection 2.4.4 Determining Trigonometric Ratios Using a Calculator

Activity 2.4.9.

\(\textbf{Work in pairs}\)
What you require:
  • Scientific calculators or any other calculator having \(sin\text{,}\)\(cos\) and \(tan\) battons.
  • Protractor and ruler (for optional verification with a drawn triangle).
  • Worksheet with a table.
  1. Turn on your scientific calculator.
  2. Ensure your calculator is set to degree mode (not radians).
  3. For each given angle (0°, 25°, 30°, etc.), do the following;
    • Press the sin button followed by the angle, then note the value.
    • Press the cos button followed by the angle, then note the value.
    • Press the tan button followed by the angle, then note the value.
  4. Record all values in the table below.
    • Use a calculator to find the sine, cosine, and tangent of the given angles, and fill in the table.
      Angle (\(^\circ\)) \({\color{blue} sin}\) \({\color{blue} cos}\) \({\color{blue} tan}\)
      \(0^\circ\)
      \(25^\circ\)
      \(30^\circ\)
      \(45^\circ\)
      \(60^\circ\)
      \(75^\circ\)
      \(90^\circ\)
  5. Observe and Answer
    • Observe the values of sin in your table. Do they increase or decrease?
    • Compare the cosine values for different angles.
    • Why does \(tan\,90^\circ\) display a syntax error?
  6. Discuss your work with other learners.
\(\textbf{Key Takeaway}\)
When given an acute angle, a calculator can be used to determine these ratios accurately.
\(\textbf{How to determine trigonometric ratios using a calculator}\text{.}\)
calculator
  1. Ensure the calculator is in degree mode.
    • Press the "MODE" button and select "DEG" (if using a scientific calculator).
  2. Enter the angle value.
    • For example, to find \(sin\,30^\circ\text{,}\) type:
      • Press sin \(\to\) Press 30 \(\to\) Press =
      • The calculator should display \(0.5\) or some calculator will display \(\frac{1}{2}\text{.}\)

Example 2.4.18.

Use calculator to find the following;(write your answer to \(\textbf{4 decimal places}\)).
\(sin\,40^\circ \quad cos\, 40^\circ \quad tan\,40^\circ\)

Solution.

Ensure the calculator is in degree mode
  1. \(sin\,40^\circ\)
    Press sin \(\to\) Press 40 \(\to\) Press =
    \(sin\,40^\circ=0.6428\)
  2. \(cos\,40^\circ\)
    Press cos \(\to\) Press 40 \(\to\) Press =
    \(cos\,40^\circ=0.7660\)
  3. \(tan\,40^\circ\)
    Press tan \(\to\) Press 40 \(\to\) Press =
    \(tan\,40^\circ=0.8391\)

Example 2.4.19.

Find \(sin\,25^\circ \quad cos\, 25^\circ \quad tan\,25^\circ\) using calculator .

Solution.

  • \(sin\,25^\circ\)
    Press sin \(\to\) Press 25 \(\to\) Press =
    \(sin\,25^\circ=0.4226\)
  • \(cos\,25^\circ\)
    Press cos \(\to\) Press 25 \(\to\) Press =
    \(cos\,25^\circ=0.9063\)
  • \(tan\,25^\circ\)
    Press tan \(\to\) Press 25 \(\to\) Press =
    \(tan\,25^\circ=0.4663\)
\(\textbf{Exercises}\)
Use a calculator to determine the following trigonometric ratios:
  1. Find \(sin\,35^\circ \quad cos\, 35^\circ \quad tan\,35^\circ\text{.}\)
  2. Find \(sin\,50^\circ \quad cos\, 50^\circ \quad tan\,50^\circ\text{.}\)
  3. Find \(sin\,15^\circ \quad cos\, 15^\circ \quad tan\,15^\circ\text{.}\)
  4. Find \(sin\,75^\circ \quad cos\, 75^\circ \quad tan\,75^\circ\text{.}\)

Subsection 2.4.5 Application of Trigonometric Ratios

In this section you will learn how trigonometry are used in real life situation and many more.

Subsubsection 2.4.5.1 Trigonometric Ratios to Angles of Elevation and Depression

Activity 2.4.10.
\(\textbf{Work in groups}\)
What you require:
  • Measuring tape or meter stick.
  • Protractor or paper tube.
  • Calculator (or table of trigonometric ratios).
  • Paper and pencil.
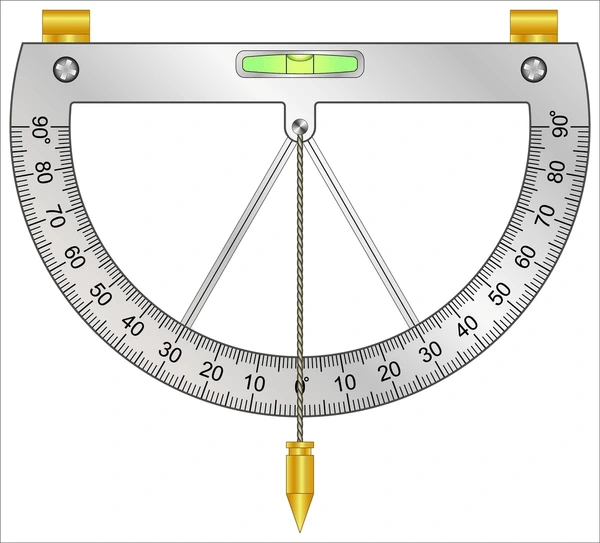
  • Use a clinometer, which is made from a string with a weight or rock attached, like the one shown below.
    clinometre
  1. Find a tall object around your suraounding e.g tree, building, flagpole, etc.
  2. Measure the distance from the base of the object to your position. Record this distance.
  3. Use your clinometer to measure the angle of elevation from your eye level to the top of the object. Record the angle.
  4. Draw a right triangle representing the situation. Label the distance you measured, the angle of elevation, and the unknown height of the object.
  5. Decide which trigonometric ratio (sine, cosine, or tangent) you need to use to find the height.
  6. Use the appropriate trigonometric ratio and the measured distance and angle to calculate the height of the object. Show your work
  7. Write down your calculated height. Compare your result with your partner’s or other groups’ results. Discuss any differences.
    NO Object Observed (e.g tree) Distance from Base (meters) Angle of Elevation (degrees) Calculation (Show Work) Calculated Height (meters)
    \(1\)
    2
    \(3\)
\(\textbf{Extended Activity }\)
Activity 2.4.11.
\(\textbf{Individual work}\)
What you require: Your homemade clinometer, a ruler or measuring tape, a notebook and pen and a friend (optional, but fun!)
  1. Climb up to a higher place like a step, a balcony, or a small hill
  2. Hold the clinometer at eye level, and look through it toward an object on the ground (like a cone, stone, or your friend’s shoes).
  3. Watch the string and record the angle where it crosses the scale. That’s your angle of depression!
  4. Measure the height from your eyes to the ground (that’s your vertical distance).
    Calculate how far the object is from the base of your standing point.
  5. Share and discuss your work with your classmates.
\(\textbf{Key Takeaway}\)
A \(\textbf{clinometer}\) (or inclinometer) is a tool used to measure the angle of elevation (looking up) and the angle of depression (looking down).
The figure below shows a person standing on the ground, looking at an object at the top. This forms an angle of elevation. When looking down from a higher point, it forms an angle of depression.
The dashed line is the horizontal line.
  • \(\textbf{Angle of Elevation:}\) The angle measured upward from a horizontal line to an object above.
  • \(\textbf{Angle of Depression:}\) The angle measured downward from a horizontal line to an object below.
Example 2.4.20.
A person stands \(20\,m\) away from a tree. The angle of elevation from their eyes is (\(1.6m\) above the ground) to the top of the tree is \(35^\circ\text{.}\) Find the height of the tree.
Solution.
Look at the scetch below;
Use \(tan\,\theta\)
\begin{align*} tan\,35^\circ=\amp \frac{\text{Tree height}-1.6 \,m}{20\,m} \\ \text{Tree height}=\amp (20 \times tan\,35^\circ)+1.6 \\ =\amp(20 \times 0.7002)+1.6 \\ =\amp 14+1.6 \\ = \amp 15.6\,m \end{align*}
Example 2.4.21.
A lighthouse is \(50\,m \) tall. A sailor spots the top of the lighthouse at an angle of elevation of \(^\circ\text{.}\) How far is the ship from the base of the lighthouse?
Solution.
Look at the scetch below;
Use \(tan\)
\begin{align*} tan\,25^\circ=\amp \frac{50\,m}{\text{Base}} \\ \text{Base}=\amp \frac{50}{tan\,25^\circ} \\ = \amp \frac{50}{0.4663} \\ =\amp 107.2\,m \end{align*}
Example 2.4.22.
A hiker stands on top of a hill that is \(120\,cm\) high and looks down at a cabin in a valley. The angle of depression to the cabin is \(40^\circ\text{.}\) Calculate the horizontal distance from the hiker to the cabin.
Solution.
See the figure below;
Use \(tan\text{:}\)
\begin{align*} tan\,40^\circ=\amp \frac{120\,cm}{\text{Cabin distance}} \\ \text{Cabin distance}=\amp \frac{120}{tan\,40^\circ} \\ =\amp \frac{120}{0.8391} \\ =\amp 143\,cm \end{align*}
\(\textbf{Exercises}\)
  1. A ladder is leaning against a wall, forming an angle of \(60^\circ\) with the ground. If the ladder is \(10\,\) meters long, how high does it reach on the wall? Draw a right-angled triangle to represent the situation
  2. If the angle of elevation is \(30^\circ\) and the distance to the object is \(50\,m\text{,}\) then the height above eye level is:
  3. A drone flies to a height of \(80\) meters above the ground. The angle of depression from the drone to a person standing on the ground is \(30^\circ\text{.}\) Find the horizontal distance between the person and the drone’s projection on the ground. Sketch the problem.
  4. A surveyor is standing \(50\) meters away from the base of a mountain. The angle of elevation to the peak of the mountain is \(30^\circ\text{.}\) Calculate the height of the mountain above the surveyor’s eye level.
  5. If the angle of depression is \(40^\circ\) and the horizontal distance to the object is \(20\,m\text{,}\) the vertical top is:
\(\textbf{Technology Integration: Exploring Trigonometric Ratios}\)
To learn more on trigonometric ratios, find these interactive and insightful resources:
  1. Khan Academy – Interactive Learning
    Learn trigonometric ratios in right triangles through step-by-step tutorials and hands-on exercises.
  2. Trigonometry Short Course Guide
    A well-structured PDF with in-depth explanations and examples to strengthen your grasp of trigonometry.
  3. YouTube Video – Visual Explanation
    Gain a clear and concise understanding of trigonometric ratios with this engaging video tutorial.
PrevTopNext