Skip to main content
Contents Dark Mode Prev Up Next \(\newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Section 2.6 Area of a Part of a Circle
In Grade 8, you learned how to find the area and arc length of a sector.
Now, you’ll go a step further and discover how to find the area of different parts of a circle.
the area of an annulus (a ring shape),
the area of an annular sector (a slice of a ring),
and the area where circles overlap.
Subsection 2.6.1 Area of an Annulus
Activity 2.6.1 .
\(\textbf{Work in groups }\)
What you require: Circular objects (e.g., two different-sized cups, lids, or rings), ruler or measuring tape and pen and paper (or a calculator).
Look around your surroundings and find two circular objects that can fit inside each other (e.g., two different-sized bowls, two bottle caps, or two CDs).
Place the smaller object inside the larger one to visualize the annulus (ring shape).
Measure the radius of the larger circle (
\(R\) ) from its center to the edge.
Measure the radius of the smaller circle (
\(r\) ) in the same way.
Square both radii. and record your result.
Subtract the squared radius of the smaller circle from the squared radius of the larger circle.
Multiply the result by
\(\frac{22}{7}\) or
\(3.142\)
Discuss with your group how to calculate the area of an annulus.
Try this activity with different circular objects and compare your results.
\(\textbf{Extended Activity}\)
Activity 2.6.2 .
\(\textbf{Individual work}\)
Situation: Imagine a running track built around a circular field. The track has an inner boundary (smaller circle) and an outer boundary (larger circle). The track itself forms an annulus.
A school is planning to paint the running track.
The inner radius of the track is
\(30\) meters, and the outer radius is
\(35\) meters.
The cost of painting is Ksh
\(5\) per square meter
The total cost of painting the track.
\(\textbf{Key Takeaway}\)
An
\(\textbf{annulus}\) is the region between two concentric circles that share the same center but have different radii as shown below.
The area of an annulus (a ring-shaped object) is found by subtracting the area of the smaller, inner circle from the area of the larger, outer circle.
\begin{align*}
A_\text{annulus} = \amp A_\text{outer circle} - A_\text{inner circle} \\
= \amp \pi R^2 - \pi r^2 \\
= \amp \pi (R^2 - r^2)
\end{align*}
Example 2.6.1 .
Find the area of an the annulus drawn below;
Solution .
\(R=10\,cm\) and
\(r=6\,cm\)
\begin{align*}
A= \amp \pi(R^2-r^2) \\
=\amp \pi(10^2-6^2) \\
=\amp \pi(100-36)\\
=\amp 64\pi \\
=\amp 64 \times \frac{22}{7}\\
= \amp 201.06 \,cm^2
\end{align*}
Example 2.6.2 .
A wheel has an outer radius of
\(40 \,cm\text{,}\) and its inner hub has a radius of
\(10 \,cm\text{.}\) Find the area of the wheel’s annular region.
Solution .
The outer radius of the wheel
\(= 40\,cm\text{.}\)
Inner hub radius
\(=10\,cm\)
\begin{align*}
A= \amp \pi(R^2-r^2)\\
=\amp \frac{22}{7}(40^2-10^2) \\
=\amp \frac{22}{7}(1\,600-100)\\
=\amp \frac{22}{7} \times 1\,500 \\
=\amp 4\,712.39 \,cm^2
\end{align*}
A ring-shaped garden has an outer radius of
\(12\) meters and an inner radius of
\(7\) meters. Find the area of the garden.
A circular tabletop has a hole in the middle for an umbrella. The outer radius of the table is
\(1.5 \,m\text{,}\) and the hole has a radius of
\(0.5 m\) as shown below.
Find the area of the tabletop.
A circular swimming pool has an outer radius of
\(8\) meters, and a smaller circular island is in the center with a radius of
\(2\) meters. Find the area of the water surface.
A steel pipe has an outer diameter of
\(80\) units and an inner diameter of
\(60\) units, what is the area of the cross-section?
Find the area of the figure below; use
\(\pi=3.142\)
What is the area of the annulus shown; (Leave your answer to
\(3\) significant figures).
Subsection 2.6.2 Area of a Sector of a Circle
Activity 2.6.3 .
\(\textbf{Work in groups}\)
A graph paper and a razorblade or a pair of scissor✂️
Draw a circle of radius
\(7 \, cm\) on a graph paper.
Cut out the circle along its boundary.
Mark the centre of the circle.
Measure an angle of
\(30^\circ\) at the centre and cut out as shown.
Estimate the area by counting the number of squares enclosed by the arc and the two radii of the circle.
Express the angle of the sector (\(30^\circ\) ) as a fraction of the angle at the centre of the circle (\(360^\circ\) ).
Multiply the fraction obtained in (6) by the area of the circle.
Discuss and share the result with other groups.
\(\textbf{Key Takeaway}\)
A
\(\textbf{sector}\) is a region bounded by two radii and an arc.
Minor sector is one whose area is less than a half of the area of the circle.
Major sector is onewhose area is greater than a half of the area of the circle.
\begin{align*}
\text{Area of a Sector}=\amp \frac{\theta}{360} \times \pi r^2
\end{align*}
\(\theta\) is in degrees,
\(r\) is the radius of the circle,
\(\displaystyle \pi \,≈ \,3.142\, \text{or} \, \frac{22}{7}.\)
Example 2.6.3 .
Find the area of a sector of a circle of radius
\(7 \,cm\) if the angle subtended at the centre is
\(90^\circ\text{.}\)
Solution .
The values given are,
\(\theta=90^\circ \, , \, r= 7\,cm\)
\(\text{Area}= \frac{\theta}{360} \times \pi r^2\)
\begin{align*}
\text{Area}=\amp \frac{90}{360} \times \frac{22}{7} \times ( 7^2)\\
=\amp \frac{1}{4} \times \frac{22}{7} \times 49 \\
=\amp \frac{1}{4} \times 22 \times 7\\
=\amp 38.5 \,cm^2
\end{align*}
Example 2.6.4 .
Find the area of a sector of a circle shown below;(use
\(\pi=3.142\) )
Solution .
The values given are,
\(\theta=45^\circ \, , \, r= 10\,cm\)
\(\text{Area}= \frac{\theta}{360} \times \pi r^2\)
\begin{align*}
\text{Area}\amp \frac{45}{360} \times 3.142 \times ( 10^2)\\
=\amp \frac{1}{8} \times 3.142 \times 100 \\
=\amp 39.275 \,cm^2
\end{align*}
Example 2.6.5 .
The shaded region in the figure below shows the area swept out on a flat windscreen by a wiper. Calculate the area of this region.
Solution .
The area of the rigion is goten by subtracting the
\(\textbf{Area of the smaller sector}\) from
\(\textbf{Area of the larger sector}\) .
Use
\(\text{Area}= \frac{\theta}{360} \times \pi r^2\)
\(\textbf{Area of the larger sector}\)
\begin{align*}
R= \amp 16\,cm + 4\,cm \\
= \amp 20\,cm
\end{align*}
\begin{align*}
\theta= \amp 120^\circ
\end{align*}
\begin{align*}
A=\amp \frac{120}{360} \times \frac{22}{7} \times 20^2 \\
=\amp \frac{1}{3} \times \frac{22}{7} \times 400\\
=\amp 419.047619 \,cm^2
\end{align*}
\(\textbf{Area of the smaller sector}\)
\begin{align*}
r= \amp 16\,cm
\end{align*}
\begin{align*}
\theta= \amp 120^\circ
\end{align*}
\begin{align*}
A=\amp \frac{120}{360} \times \frac{22}{7} \times 16^2 \\
=\amp \frac{1}{3} \times \frac{22}{7} \times 256\\
=\amp 268.19047 \,cm^2
\end{align*}
\begin{align*}
\text{Area of the region}=\amp \textbf{Area of the larger sector} -\textbf{Area of the smaller sector}\\
=\amp 419.047619 \,cm^2- 268.19047 \,cm^2\\
=\amp 150.85714\,cm^2
\end{align*}
A sector of a circle of radius
\(r\) is subtended at the centre by an angle of
\(\theta\text{.}\) Calculate the area of the sector if:
\(\displaystyle r=10\,m ,\quad \theta=264^\circ\)
\(\displaystyle r=8.4\,cm ,\quad \theta=40^\circ\)
\(\displaystyle r=1.4\,cm ,\quad \theta=80^\circ\)
The area of a sector of a circle is
\(\,cm^2\) . Find the radius of the circle if the angle subtended at the centre is
\(140^\circ\text{.}\) (Take
\(\pi= \frac{22}{7}\) )
A goat is tethered at the corner of a fenced rectangular grazing field. If the length of the rope is
\(21 \,m\text{,}\) what is its grazing area?
Shown below is a sector of a circle, with radius
\(x\,cm\)
The area of the sector is
\(18 \pi \,cm^2\)
A sector has an angle of
\(\frac{\pi}{3}\) radians and a radius of
\(8 \,cm\text{.}\) Find its area.
Subsection 2.6.3 Area of an Annular Sector
Activity 2.6.4 .
\(\textbf{Work in groups}\)
Two circular paper cutouts (one smaller, one larger),
Take two circular cutouts of different sizes but with the same center.
Use a protractor to mark the same central angle
\(\theta\) on both circles.
Cut out the corresponding sectors from both circles.
Place the smaller sector on the larger one and observe the remaining shape.
Measure and calculate the area of each sector using the formula and compare with your actual cutout.
Discuss with other groups how to get the area of the figure you have formed.
\(\textbf{Extended Activity}\)
Activity 2.6.5 .
\(\textbf{Work in groups}\)
A car wiper blade (or a picture of one) like the one drawn below;
A notebook and calculator
Find the dimensions of the following;
The length of the wiper blade.
The pivot point to the base of the wiper blade.
The angle
\(\theta\) is the angle through which the wiper moves.
\begin{align*}
A= \amp \frac{\theta}{360} \times \pi(R^2-r^2)
\end{align*}
to calculate the area cleaned by the wiper.
Ask students in your group to observe whether the wiper covers all parts of the windshield equally.
\(\textbf{Key Takeaway}\)
An
\(\textbf{annular sector}\) is the region enclosed between two concentric sectors of a circle with different radii but the same central angle. It is similar to a sector but with a smaller sector removed from a larger one.
Having the knowledge of the area of a sector and the area of an annulus it is very easy to identify the area of an annular sector.
\(\textbf{Area of an annular sector}\)
Area of an annular sector is:
\begin{equation*}
A=\frac{\theta}{360} \times \pi(R^2-r^2)
\end{equation*}
Example 2.6.6 .
A wind turbine blade sweeps through a central angle of
\(140^\circ\text{.}\) The length of the blade is
\(50\, m\text{,}\) and the inner radius (distance from the pivot to the base of the blade) is
\(10\, m\text{.}\) Find the swept area.
Solution .
The learger radius (
\(R\) )
\(=50\,m\)
The inner radius (
\(r\) )
\(=10\,m\)
Angle subtended
\(=140^\circ\)
\begin{align*}
A= \amp \frac {140}{360} \times \pi (50^2-10^2)\\
= \amp \frac{7}{18} \times \frac{22}{7} (2\,500-100) \\
=\amp \frac{7}{18} \times \frac{22}{7} \times 2\,400\\
= \amp 2933.333333 \\
≈\amp 2\,933.3 \,m^2
\end{align*}
The turbine sweeps an area of approximately
\(2\,933.3 \,m^2\text{.}\)
Example 2.6.7 .
Find the area of the annular sector shown below. (Use
\(\pi= 3.142\) )
Solution .
\(A= \frac{\theta}{360} \times \pi(R^2-r^2)\)
\begin{align*}
A=\amp \frac{60}{360} \times \pi(12^2-8^2) \\
=\amp \frac{60}{360} \times 3.142 (144-64)\\
=\amp \frac{1}{6} \times 3.142\times 80 \\
=\amp \frac{1}{3} \times 3.142 \times 40\\
= \amp 41.89333333 \\
≈\amp 41.89\,cm^2
\end{align*}
A clock’s minute hand moves
\(150^\circ \) in
\(25\) minutes. The minute hand is
\(15 \,cm\) long, and the inner radius is
\(5 \,cm\) Calculate the cleaned area.
A windshield wiper moves through
\(110^\circ\text{.}\) The blade is
\(45 \,cm\) long, and the pivot distance is
\(15\, cm\text{.}\) Calculate the cleaned area.
Outer radius
\(=40 \,cm\)
Inner radius
\(r=10\,cm\)
Central angle
\(=120^\circ\)
Find the area cleaned by the wiper.
A mechanical arm sweeps through 180°. The outer radius is
\(8\, m\text{,}\) and the inner radius is
\(2 \,m\text{.}\) Determine the area covered.
The shaded region in the figure below shows the area swept out on a flat windscreen by a wiper. Calculate the area of this region.
Subsection 2.6.4 Area of a Segment of a Circle
Activity 2.6.6 .
\(\textbf{Work in groups}\)
A worksheet with given radii and angles
Use a compass to draw a circle of radius
\(r\text{.}\)
Draw a chord across the circle using a ruler.
Use a protractor to measure the angle subtended at the center by the chord.
Find the area of the segment part and record your results.
Perform the same process for different chords and angles eg
\(70^\circ, \,90^\circ,\,120^\circ,\,150^\circ...\)
Discuss your work with other learners in your class.
\(\textbf{Key Takeaway}\)
A
\(\textbf{segment} \) is the region of a circle bounded by a chord and an arc as shown in the figure below.
The shaded region is a segment of the circle with centre
\(O\) and the radius
\(q\)
\(\textbf{Area of a segment of a circle.}\)
The area of a segment is given by;
\(\text{Area of a segment}=\text{Area of sector}-\text{Area of triangle}\)
Example 2.6.8 .
A chord in a circle of radius
\(7\, cm\) subtends an angle of
\(75^\circ\) at the center as shown below. Find the area of the segment.
Solution .
To find the area of the segment, you the area of the triangle and subtract from the area of the sector.
\(\textbf{Area of sector }\)
\(A= \frac{\theta}{ 360} \times \pi r^2\)
\begin{align*}
A=\amp \frac{75^\circ}{ 360} \times \frac{22}{7} \times 7^2 \\
=\amp \frac{5}{24} \times \frac{22}{7} \times 49\\
=\amp \frac{385}{12} \\
=\amp 32.0833 \,cm^2
\end{align*}
\(\textbf{Area of a triangle }\)
\(A= \frac{1}{2} ab sin \,\theta\)
Where
\(a=7\,cm \,\text{and} \,b= 7 \,cm\)
\begin{align*}
A=\amp \\
=\amp \frac{1}{2} \times 7 \times 7\times \times sin \,75^\circ\\
=\amp \frac{1}{2} \times 49 \times sin \,75^\circ\\
=\amp 23.6652 \,cm^2
\end{align*}
\begin{align*}
A= \amp 32.0833 \,cm^2- 23.6652 \,cm^2 \\
= \amp 8.4181\,cm^2
\end{align*}
Example 2.6.9 .
A chord XY of length
\(14 \,cm\) is drawn in a circle with centre O and radius
\(8 cm\text{,}\) as in the figure below
the area of the sector OXPY.
the area of the minor segment.
the area of the major segment.
Solution .
Given a circle with center
\(O\text{,}\) radius
\(8\) cm, and a chord
\(XY\) of length
\(14\,cm\) , we find the required values step by step.
Finding the Distance
\(\text{ON}\)
Since ON is the perpendicular bisector of XY, we use the right triangle ONX where:
\begin{align*}
\text{OX}=\amp 8\,cm (\text{radius}) \\
\text{NX}=\amp \frac{\text{XY}}{2} \\
= \amp \frac{12}{2} \\
= \amp 7\,cm
\end{align*}
Using Pythagoras’ Theorem in
\(\triangle\) ONX:
\begin{align*}
\text{ON}^2+ \text{NX}^2 =\amp \text{OX}^2\\
\text{ON}^2+ 7^2= \amp 8^2 \\
\text{ON}^2+ 49= \amp 64 \\
\text{ON}^2=\amp 64-49\\
\text{ON}^2= \amp 15 \\
\text{ON} =\amp \sqrt{15} \\
≈\amp 3.87 \,cm
\end{align*}
Finding the area of sector OXPY.
Finding the
\(\angle\) XOY which is given by:
\begin{align*}
cos\,\theta= \amp (\frac{\text{XN}}{\text{XO}} )\\
=\amp \frac{7}{8} \\
=\amp 0.875 \\
\theta=\amp cos^{-1}(0.875) \\
=\amp 28.9550^\circ
\end{align*}
therefor,
\(\angle \text{XOY}= 28.9550^\circ\times 2\)
\begin{equation*}
=57.9100^\circ
\end{equation*}
\begin{align*}
A=\amp \frac{\theta}{360} \times \pi r^2\\
=\amp \frac{57.9100}{360} \times \pi 8^2 \\
=\amp \frac{57.9100}{360} \times \frac{22}{7} \times 64\\
=\amp 32.3561 \,cm^2
\end{align*}
Therefore, area of sector OXPY
\(= 32.3561 \,cm^2\)
Finding the area of triangle OXY
\begin{align*}
\text{Area}= \amp \frac{1}{2} \times \text{base} \times \text{height} \\
=\amp \frac{1}{2} \times 14 \times 3.87 \,cm \\
= \amp 7 \times 3.87 \,cm \\
=\amp 27.09 \,cm^2
\end{align*}
Finding the area of the minor segment.
\(\text{Area of minor segment}=\text{Area of sector}- \text{Area of} \triangle \text{OXY}\)
\begin{align*}
\text{Area of minor segment}=\amp \\
=\amp 32.3561 \,cm^2-27.09 \,cm^2 \\
=\amp 5.2661\,cm^2
\end{align*}
Finding the area of the major segment
Area of major segment
\(=\) Total circle area
\(-\) Area of minor segment
\begin{align*}
A= \amp \pi r^2 \\
=\amp \frac{22}{7} \times 8^2 \\
=\amp \frac{22}{7} \times 64 \\
=\amp 201.1429 \,cm^2
\end{align*}
Therefore, Area of major segment is
\begin{align*}
= \amp 201.1429 \,cm^2- 5.2661\,cm^2\\
=\amp 195.8768\,cm^2
\end{align*}
In the figure below, ADC is a chord of a circle with centre O passing through A, B and C. BD is a perpendicular bisector of AC. AD
\(=
4 \,cm\) and BD
\(= 2 \,cm\text{.}\)
the radius OA of the circle.
the area of the sector OABC.
the area of the segment ABCD
A circular table has a radius of
\(15 \,cm\text{.}\) A slice of cake is cut out, forming a
\(75^\circ \) segment. Find the area of the cake slice not covered by the straight cut
A wheel of a car has a radius of
\(30 \,cm\text{.}\) A mudguard covers a
\(60^\circ\) segment of the wheel. Find the area of the covered segment.
A circular park has a radius of
\(20\) meters. A walking path cuts across the park, forming a chord that subtends an angle of
\(120^\circ\) at the center as shown below.
A chord XY subtends an angle of
\(120^\circ\) at the centre of a circle of radius
\(13\, cm\text{.}\) Calculate the area of the minor segment.
Subsection 2.6.5 Area of Common Region between two Intersecting Circles
Activity 2.6.7 .
\(\textbf{work in groups}\)
What you require; Compass, ruler, pencil, graph paper and Calculator.
Use a compass to draw a circle with a radius of
\(5\,cm\) centered at point
\(O\text{.}\)
From a point
\(2 \,cm\) to the right of
\(O\text{,}\) draw another circle with the same radius (
\(5 cm\) ).
This should create an overlapping region.
Name the intersection points of the two circles as P and Q.
Lightly shade the overlapping region between the two circles.
Finding the area of the common region.
How does the distance between centers affect the common area?
Discuss your result with other learners in class.
\(\textbf{Key Takeaway}\)
The
\(\textbf{common region between two intersecting circles}\) refers to the overlapping area shared by both circles.
It is formed when two circles of different or equal radii intersect at two distinct points as shown below.
The area of the common region can be found by:
Calculating the area of the two circular segments formed by the chord joining the intersection points.
Sum the areas of the two segments.
\begin{align*}
A= \amp A_\text{segment 1}+ A_\text{segment 2}
\end{align*}
The figure below shows the two segments.
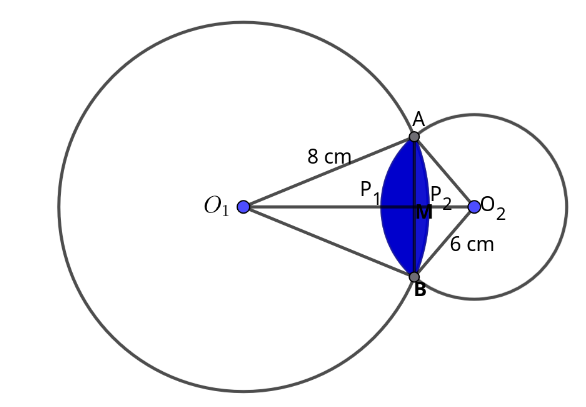
Example 2.6.10 .
The figure below shows two circles of radii
\(8\,
cm\) and
\(6 \,cm\) with centres
\(O_1\) and
\(O_2\) respectively. The circles intersect at points A and B. The lines
\(O_1O_2\) and AB are perpendicular to each other. If the common chord AB is
\(9 \,cm\text{,}\) calculate the area of the shaded region.
Solution .
From
\(\triangle AO_1M\text{;}\)
\begin{align*}
O_1M=\amp \sqrt{8^2-4.5^2} \\
= \amp \sqrt{43.75} \\
=\amp 6.14\,cm
\end{align*}
From
\(\triangle AO_2M\text{;}\)
\begin{align*}
O_2M=\amp \sqrt{6^2-4.5^2} \\
= \amp \sqrt{15.75} \\
=\amp 3.969\,cm
\end{align*}
The area of the shaded region is the sum of the areas of segments
\(AP_1B\) and
\(AP_2B\text{.}\) \(\text{Area of segment }AP_1B = \text{area of
sector }C_2AP_1B – \text{area of }\triangle O_2AB.\)
\begin{align*}
\angle AO_2M=\amp\frac{AM}{AO_2} \\
=\amp \frac{4.5}{6} \\
=\amp 0.75 \\
\angle =\amp sin^{-1} \,(0.75) \\
= \amp 48.59^\circ
\end{align*}
\begin{align*}
\angle AO_2B=\amp 2\angle AO_2M\\
=\amp 2 \times 48.59^\circ \\
=\amp 97.18^\circ
\end{align*}
Area of segment
\(AP_1B\)
\begin{align*}
= \amp \frac{97.18}{360} \times 3.142 \times 6^2\\
=\amp 30.53
\end{align*}
Area of triangle.
\begin{align*}
=\amp\frac{1}{2} \times 9 \times 3.969 \\
=\amp 17.86
\end{align*}
\begin{align*}
\text{Area of segment}AP_1B=\amp 30.53 -17.86\\
=\amp 12.67\,cm^2
\end{align*}
\(\text{Area of segment }AP_2B = \text{area of
sector }0_1AP_2B – \text{area of }\triangle O_1AB.\)
\begin{align*}
\angle AO_1M=\amp\frac{AM}{AO_1} \\
=\amp \frac{4.5}{8} \\
=\amp 0.5625 \\
\angle =\amp sin^{-1} \,(0.5625) \\
= \amp 34.23^\circ
\end{align*}
\begin{align*}
\angle AO_1B=\amp 2\angle AO_1M\\
=\amp 2 \times 34.23^\circ \\
=\amp 68.46^\circ
\end{align*}
Area of segment
\(AP_2B\)
\begin{align*}
= \amp \frac{68.46}{360} \times 3.142 \times 8^2\\
=\amp 38.24
\end{align*}
Area of triangle.
\begin{align*}
=\amp\frac{1}{2} \times 9 \times 6.614 \\
=\amp 29.76
\end{align*}
\begin{align*}
\text{Area of segment}AP_2B=\amp 38.24-29.76\\
=\amp 8.48\,cm^2
\end{align*}
Therefore, area of the shaded region is given by;
\(\text{Area of segment}AP_1B+\text{Area of segment}AP_2B\)
\begin{align*}
=\amp 12.67\,cm^2+8.48\,cm^2\\
=\amp 21.15\,cm^2
\end{align*}
Example 2.6.11 .
The figure below shows two intersecting circles of radius
\(10\,cm\) each with centre
\(P_1\) and
\(P_2\text{.}\) The length of
\(P_1\) and
\(P_2\) is
\(6\,cm\text{.}\) (Take
\(\pi=3.142\) )
the length of the common chord
\(\textbf{PQ}\text{.}\)
the area common to the two circles.
Solution .
Two intersecting circles with radius
\(r=10,cm.\text{.}\)
Distance between the centers:
\(P_1P_2=6\,cm\text{.}\)
The common chord PQ is perpendicular to
\(P_1P_2\) at
\(T\) (the midpoint of PQ).
Finding the Length of the Common Chord PQ
Applying the Right-angled triangle property
Since the chord PQ is perpendicular to the line joining the centers, we can analyze the right-angled triangle
\(P_1TP\text{.}\)
Using the Pythagorean theorem in \(\triangle P_1TP\text{;}\)
\begin{equation*}
P_1P^2=P_1T^2+PT^2
\end{equation*}
\(P_1T=\frac{P_1P_2}{2}=\frac{6}{2}=3\,cm\text{.}\)
\begin{align*}
10^2=\amp 3^2+PT^2 \\
100=\amp 9+PT^2 \\
PT^2=\amp 91 \\
PT=\amp 91 \\
=\amp \sqrt{91} \\
=\amp 9.54 \,cm
\end{align*}
\begin{align*}
\text{PQ}=\amp 2 \times 9.54 \,cm \\
=\amp 19.08\, cm
\end{align*}
Finding the common area between the two circle.
The common area consists of two identical circular segments, each subtended by the central angle
\(2\theta\) at
\(P_1\) or
\(P_2\text{.}\)
\begin{align*}
cos\,\theta=\amp \frac{P_1T}{P_1P} \\
=\amp \frac{3}{10} \\
= \amp 0.3 \\
\theta= \amp cos^{-1}\,0.3\\
= \amp 72.54^\circ
\end{align*}
\(\angle\,P_1=\angle \,P_2= 2\times 72.54^\circ\)
\begin{equation*}
=145.08^\circ
\end{equation*}
Finding the segmet of
\(P_1 \,\text{and} \, P_1\text{.}\) Since the segment are the same, it implies that area of segment
\(P_1=P_2\text{.}\)
\(\text{Area of segment}=\text{area of sector}-\text{area of triangle}\)
\begin{align*}
A=\amp \frac{145.08^\circ}{360} \times 3.142 \times 10^2\\
= \amp 126.62 \,cm^2
\end{align*}
\begin{align*}
A=\amp \frac{1}{2} \times 10 \times 10 \times sin\,145.08\\
= \amp \frac{1}{2} \times 10^2 \times sin\,145.08\\
= \amp 28.62\,cm^2
\end{align*}
Area of segment
\(= 126.62 \,cm^2-28.62\,cm^2\)
\begin{equation*}
=98.00\,cm^2
\end{equation*}
Area of the common region
\(= 2\times 98.00\,cm^2\)
\begin{equation*}
196.00\,cm^2
\end{equation*}
If two circles of radius
\(r\) overlap such that their centers are at a distance
\(0.5\,r\text{,}\) express the overlapping area in terms of
\(r\text{.}\)
Two circular traffic islands of radius
\(10\) meters overlap so that the centers are
\(12\) meters apart. The angle subtended at the center of each circle by the chord of intersection is
\(120^\circ\text{.}\) Find the area of the overlapping region.
Find the area of the figure below;
In the Olympic symbol, circles of radius
\(5 \,cm\) overlap, forming intersections. If the central angle corresponding to the common region is
\(90^\circ\text{,}\) find the area of the intersection.
During a rare planetary alignment, two planets appear as overlapping circles in the sky. If both have an apparent radius of
\(5000\, km\text{,}\) and their centers are
\(6000 \,km\) apart, with a central angle of
\(145^\circ\text{,}\) find the overlapping shadow area visible from Earth.
\(\textbf{Technology Integration: Exploring Areas of Part of a Circle}\)
To deepen your understanding of how to find the area of different parts of a circle, explore the following interactive and insightful resources:
YouTube – Shifting Grades Online School
This video lesson offers a visual and step-by-step explanation on how to find the area of parts of a circle. It’s ideal for learners who prefer guided instruction with examples.
Learn about circle sectors and other related topics with this clear and concise tutorial. Great for quick revision or reinforcing concepts.
BBC Bitesize – Guide on Circles
This interactive webpage from BBC Bitesize explains how to calculate the area of parts of a circle using helpful visuals and explanations.
GeoGebra – Interactive Geometry Tool
Use GeoGebra to explore and manipulate circle diagrams in real time. You can adjust radii and angles to see how the area of a sector or annulus changes perfect for visual learning and experimentation.