Skip to main content
Contents Dark Mode Prev Up Next \(\newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Section 1.2 Indices and Logarithms
Subsection 1.2.1 Indices
Introduction.
Mathematics involves working with very large and very small numbers, which can be simplified using indices. An
\(index\) (plural,
\(indices\) ) also called
\(exponent\) or
\(power\) is a way of writing repeated multiplication of the same number.
Why Are Indices Important?
Indices are widely used in:
Scientific notation writing, where numbers are sometimes very large and sometimes very small, such as the speed of light or the size of an atom.
Physics and Engineering to understand exponential growth and decay rates, such as radioactive decay and population growth.
Finance and money in calculating compound interest.
Subsubsection 1.2.1.2 Laws of Indices
When we need to work with indices efficiently, we use a set of rules called the Laws of Indices. They are useful in carrying out operations involving indices.
When multiplying numbers with the same base, add their powers.
i.e
\(a^m \times a^n = a^{m + n}\)
\begin{equation*}
3^2 \times 3^4 = 3^{2 + 4}
\end{equation*}
\begin{equation*}
= 3^6
\end{equation*}
When dividing numbers with the same base, subtract their powers.
i.e
\(\frac {a^m}{a^n}\) =
\(a^{m-n}\)
\begin{equation*}
5^7 \div 5^3 = \frac {5^7}{5^3} = \frac {5 \times 5 \times 5 \times 5 \times 5 \times 5 \times 5}{5 \times 5 \times 5}
\end{equation*}
\begin{equation*}
= 5^{(7 - 3)}
\end{equation*}
\begin{equation*}
= 5^4
\end{equation*}
When raising a power to another power, multiply the powers.
i.e
\((a^m)^n\) =
\(a^{(m \times n)}\)
\begin{equation*}
{(3^2)}^3 = (3 \times 3) \times (3 \times 3) \times (3 \times 3)
\end{equation*}
\begin{equation*}
=3^{(2 \times 3)}
\end{equation*}
\begin{equation*}
= 3^6
\end{equation*}
d) Power of a Product Law
When raising a power to a product factor, multiply the power to all factors inside the bracket.
i.e
\((ab)^n\) =
\(a^n \times b^n\)
\begin{equation*}
(2 \times 3)^3 = 2^3 \times 3^3
\end{equation*}
\begin{equation*}
= 8 \times 27
\end{equation*}
\begin{equation*}
= 216
\end{equation*}
A fractional power represents a root.
i.e
\((a^{\frac {m}{n}})\)
\begin{equation*}
(a^m)^{\frac {1}{n}} = \sqrt [n]{a^m}
\end{equation*}
\begin{equation*}
= \sqrt [3]{8^1}
\end{equation*}
\begin{equation*}
=2
\end{equation*}
\begin{equation*}
8 = 2 \times 2 \times 2 = 2^3
\end{equation*}
\begin{equation*}
8^{\frac {1}{3}} = {(2^3)}^{\frac {1}{3}}
\end{equation*}
\begin{equation*}
= 2^{(3 \times \frac {1}{3})}
\end{equation*}
\begin{equation*}
= 2
\end{equation*}
\begin{equation*}
(\frac {a}{b})^3 = \frac {a^3}{b^3}
\end{equation*}
\begin{equation*}
(\frac {4}{5})^3 = \frac {4^3}{5^3}
\end{equation*}
\begin{equation*}
= \frac {64}{125}
\end{equation*}
Table 1.2.2. Summary of the Laws of Indices
Law
\(Expression\) \(Example\)
Product Law
\(a^m \times a^n = a^{(m + n)}\) \(2^3 \times 2^4 = 2^{(3 + 4)} = 2^7 = 128\)
Quotient Law
\(a^m \div a^n = a^{(m - n)}\) \(5^7 \div 5^3 = 5^{(7 - 3)} = 5^4\)
Power of a Power Law
\((a^m)^n = a^{(m \times n)}\) \((3^2)^3 = 3^{(2 \times 3)} = 3^6\)
Power of a Product Law
\((a \times b)^n = a^n \times b^n\) \((2 \times 3)^3 = 2^3 \times 3^3 = 216\)
Fractional Powers
\(a^{(\frac {m}{n})} = n\sqrt {(a^m)}\) \(8^{(\frac {1}{3})} = 3 \sqrt {8} = 2\)
The laws apply only when the bases are the same
Activity 1.2.2 .
Materials Needed: A pen and a notebook
Each group gets a set of index question (on flashcards or written on the board).
Write the question on your notebook
Simplify using the laws of indices that applies to your question.
Each group to present their working to the class.
Example 1.2.3 .
Solution .
\begin{equation*}
2^3 = ( 2 \times 2 \times 2 )
\end{equation*}
\begin{equation*}
2^4 = ( 2 \times 2 \times 2 \times 2 )
\end{equation*}
\begin{equation*}
( 2 \times 2 \times 2 ) \times ( 2 \times 2 \times 2 \times 2 )
\end{equation*}
Count the total number of factors
\begin{equation*}
2^{(3+4)} = 2^7
\end{equation*}
\begin{equation*}
= 128
\end{equation*}
Exercises Exercises
1. Apply the index laws in solving the following expressions:
\(\displaystyle 2^6 \times 2^4 \qquad \qquad \qquad \qquad \text{e)}\,\, 8^3 \times 8^2 \div 8^4\)
\(\displaystyle 5^7 \div 5^3 \qquad \qquad \qquad \qquad \text{f)}\,\, (6^2 \times 6^3) \div 6^4\)
\(\displaystyle {(4^3)}^2 \qquad \qquad \qquad \qquad \qquad \text{g)}\,\, {(x^3y^2)}^4\)
\(\displaystyle \frac {9^5}{9^2} \times 9^3 \qquad \qquad \qquad \qquad \text{h)}\,\, \frac {m^8}{m^5} \times {(m^2)}^3\)
2. Mr. Gitonga is a farmer. He divides his rectangular field into smaller equal plots. The total area of the field is
\(5^8 \, \, m^2\text{,}\) and each small plot has an area of
\(5^3 \,\, m^2\text{.}\) How many smaller plots does Mr. Gitonga get? Express your answer using indices.
3. Mkurugenzi Company investments grows exponentially. It was initially worth
\(4^5\) Kenyan shillings, but after two years, it was multiplied by
\(4^3\text{.}\) Use indices to represent the total investment value after the two years.
4. Mathematics department has
\(2^6\) books that can be borrowed and the science section has
\(2^4\) books. Write an index expression for the total number of books in both sections if they were combined into a single shelf.
5. A carpenter is building square tables of different sizes. The first table he makes has an area of
\(3^2\) square metres. Each new table he builds is twice the length of the previous one.
Express the area of the second and third tables in index form.
Using the Laws of Indices, find the total area of the first three tables combined.
If the carpenter continues doubling the table size, what will be the area of the
\(5^{th}\) table?
Subsubsection 1.2.1.3 Zero and Negative Indices
Indices help us simplify repeated multiplication of the same number. But what happens when the exponent is zero or negative?
Zero Indices (Zero Exponent/Power Zero Law)
Activity 1.2.3 .
Look at the pattern below and complete the missing values:
\begin{equation*}
2^4 = 16
\end{equation*}
\begin{equation*}
2^3 = 8
\end{equation*}
\begin{equation*}
2^2 = 4
\end{equation*}
\begin{equation*}
2^1 = 2
\end{equation*}
\begin{equation*}
2^0 = ?
\end{equation*}
What pattern do you notice as the exponent decreases by
\(1\text{?}\)
What happens when the exponent reaches zero?
Can you try the same pattern with
\(3^n\text{?}\)
Any non-zero number raised to power zero is always
\(1\text{.}\)
Activity 1.2.4 .
Look at the pattern below and complete the missing values:
\begin{equation*}
3^3 = 27
\end{equation*}
\begin{equation*}
3^2 = 9
\end{equation*}
\begin{equation*}
3^1 = 3
\end{equation*}
\begin{equation*}
3^0 = 1
\end{equation*}
\begin{equation*}
3^{-1} = ?
\end{equation*}
\begin{equation*}
3^{-2} = ?
\end{equation*}
Write the answers as fractions and decimal values.
What do you notice about the negative exponents?
Can you try the same pattern using
\(5^n\text{?}\)
A negative exponent means taking the reciprocal of the base.
i.e
\(a^{-n}\) =
\(\frac {1}{a^n}\)
What do zero and negative indices represent, and how do they simplify expressions?
How do negative exponents help express very small values and implify small numbers?
Why does any nonzero number raised to power zero equal
\(1\text{?}\) What happens when the base is zero?
Where do we see numbers decreasing exponentially or repeated division in real life?
Example 1.2.4 .
The school need to make desks for grade
\(10\) students. A carpenter is cutting wooden planks for the desks. The length of each plank decreases by half as he cuts smaller sections.
Table 1.2.5. Plank Lengths and Index Notation
Cut Number Plank Length (metres) Index Notation
Original Plank
\(1\) \(2^0 = 1\)
First Cut
__
\(2^{-1}\)
Second Cut
__
\(2^{-2}\)
Third Cut
__
\(2^{-3}\)
Hint: The negative exponent represents how many times the length has been halved.
Solution .
Each cut divides the plank by
\(2\text{:}\)
The original plank is
\(2^0 = 1\) metre
The first cut halves the plank:
\begin{equation*}
2^{-1} = \frac {1}{2} metres
\end{equation*}
The second cut halves it again:
\begin{equation*}
2^{-2} = \frac {1}{2^2} = \frac {1}{4} metres
\end{equation*}
The third cut follows the same pattern:
\begin{equation*}
2^{-3} = \frac {1}{2^3} = \frac {1}{8} metres
\end{equation*}
If
\(n\) represents the number of cuts, the remaining plank length
\(L\) follows a trend which can bw represented as:
\begin{equation*}
L = 2^{-n}
\end{equation*}
\(L\) = remaining length after
\(n\) cuts
Using this formula, let’s calculate the length after
\(4\) cuts:
\begin{equation*}
L = 2^{-4} = \frac {1}{2^4}= \frac {1}{16} metres
\end{equation*}
After
\(4\) cuts, the remaining plank length is
\(\frac {1}{16}\) metres
✔ Negative indices represent repeated division.
✔ This pattern appears in real-life situations like paper folding, battery energy life, and population decay.
Exercises Exercises
1. Fill in the missing values following the same halving pattern:
Table 1.2.6. Plank Lengths and Index Notation
Cut Number Plank Length (meters) Index Notation
0 (Original Plank)
1
\(2^0\)
1
1/2
\(2^{-1}\)
2
__
\(2^{-2}\)
3
__
__
\(4\) __
__
2. In the
\(Msomii\) Community Library, the maths-book shelf has
\(64\) books. The librarian organizes the books by removing half of them every day.
Express the number of books left after
\(3\) days using indices.
How many books remain after
\(5\) days?
3. The Board of Management decided to buy a school van for Maths club in your school. The van costs Ksh
\(1,000,000\text{.}\) Its value decreases by half every
\(3\) years due to depreciation. Express the van’s value after
\(9\) years in index form and find how much the van will be worth after
\(15\) years?
4. A patient takes
\(400\) mg of a medicine. Every
\(4\) hours, the amount of medicine in the body reduces to
\(\frac {1}{2}\) of what was left.
Write an index expression for the medicine remaining after
\(12\) hours.
How much medicine remains after
\(20\) hours?
5. A school installs
\(100\) energy-saving bulbs. Every year, a quarter of them stop working and need replacement.
Write an index expression for the number of working bulbs after
\(4\) years.
How many bulbs are still functional after
\(6\) years?
Subsubsection 1.2.1.4 Applications of Indices in Real-Life situations
Example 1.2.7 .
Kakamega town’s population doubles every 10 years. If the population today is 50,000 people, what will it’s population be in 30 years time?
Solution .
Since the population doubles every
\(10\) years, we observe the following:
After
\(10\) years →
\(50, 000 \times 2\) =
\(100, 000\) people
After
\(20\) years →
\(100, 000 \times 2\) =
\(200, 000\) people
After
\(30\) years →
\(200, 000 \times 2\) =
\(400, 000\) people
Instead of calculating step by step, we can use indices.
Since the population doubles every
\(10\) years, we use the exponential growth model:
\begin{equation*}
P = P_0 \times P^{\frac {t}{10}}
\end{equation*}
\(P\) = population after
\(t\) years
\(P_0\) = Initial population
\((50 000)\)
\(t\) = number of years
\((30)\) years
The base
\(2\) represents doubling every
\(10\) years
\begin{equation*}
P = 50 000 \times 2^{\frac {30}{10}}
\end{equation*}
Since
\(\frac {30}{10} =3,\) we simplify:
\begin{equation*}
P = 50 000 \times 2^3
\end{equation*}
We now calculate
\(2^3\) ;
\begin{equation*}
2^3 = 2 \times 2 \times 2 = 8
\end{equation*}
\begin{equation*}
P = 50, 000 \times 8
\end{equation*}
\begin{equation*}
= 400, 000
\end{equation*}
In
\(30\) years time, the town’s population will be
\(400,000\) people
Exercises Exercises
1. The Science Club of Bidii Secondary School is conducting an experiment on bacteria growth. They place
\(1,000\) bacteria in a petri dish and observe that the bacteria triple every
\(5\) hours.
How many bacteria will be present after
\(10\) hours?
How many bacteria will be present after
\(20\) hours?
How long will it take for the bacteria to reach
\(243,000\text{?}\)
2. During the tree planting month in the school, the principal planted
\(3\) trees in the first week. Each week, the number of trees planted by the principle triples.
How many trees will be planted by the
\(5^{th}\) week?
How long will it take for the principal to plant at least
\(2,000\) trees?
3. Upendo Bank offers compound interest where an investment grows by a factor of
\(1.05\) per year. A person invests Ksh
\(50,000\text{.}\)
Write an index notation for the amount after
\(10\) years.
Find the total amount after
\(10\) years.
4. The storage capacity of computers has been increasing exponentially. The school library computer storage was
\(2\) GB in the year
\(2000\text{,}\) and its capacity doubles every
\(2\) years.
Write an expression using indices for the capacity after
\(8\) years.
What will the storage capacity be after
\(5\) years?
5. A doctor prescribes a medicine that reduces to
\(\frac {1}{4}\) of its original amount in the body every
\(6\) hours.
Express the remaining amount after
\(18\) hours in index form.
If the initial dosage was
\(200\) mg, calculate the amount left after
\(18\) hours.
6. The intensity of sound is measured in decibels and follows an exponential scale. If a normal conversation is
\(10^2\) times louder than a whisper and a jet engine is
\(10\) times louder than a whisper:
How many times louder is a jet engine compared to a normal conversation?
Express this in index notation.
Subsection 1.2.2 Logarithms
Why Logarithms?
In the previous section, indices allowed us to simplify very large or small numbers by expressing them in terms of powers. However, there are situations where we need to reverse this process, rather than finding the result of a power, we need to determine the exponent itself. This is where logarithms come into play.
A
\(logarithm\) is the inverse of an exponent (index). It tells us the power to which a specific base must be raised to produce a given number.
Exponent Form:
\(2^3 = 8.\)
Logarithm Form:
\(log_2 8 = 3.\)
In simpler terms, a
\(logarithm\) answers the question: "To what power must the base be raised to produce a certain number?"
Why Are Logarithms Important?
Logarithms are crucial for solving equations involving exponents. They simplify computations and are widely used in fields like:
Finance: calculating compound interest or investment growth.
Science and Engineering: understanding radioactive decay, measuring sound intensity, or modeling population growth.
Subsubsection 1.2.2.1 Logarithms notation
Activity 1.2.5 .
Work in groups: Form groups of
\(2-3\) students
Materials: A Paper/book and a pen
Pick a number from the set:
\(81, 243, 512\) or
\(1000\)
Break down the chosen number into its prime factors.
Start by dividing the number by its smallest prime factor repeatedly until only prime factors remain.
e.g. \(8 = 2 \times 2 \times 2 = 2^3\)
Express your final result in index form
Reflect on how the indices relate to logarithms:
For example,
\(2^3 =8\) translates to
\(\log_2 8 = 3.\)
Logarithms are simply another way of expressing indices. They bridge the gap between exponential and logarithmic notation:
Exponential Form:
\(a^b = c.\)
Logarithmic Form:
\(\log_a c = b.\)
\(e.g\)
\begin{equation*}
8 = 2 \times 2 \times 2 = 2^3
\end{equation*}
\begin{equation*}
4 = 2 \times 2 = 2^2
\end{equation*}
\begin{equation*}
2 = 2^1
\end{equation*}
The powers/ indices
\(3, 2, 1\) are the
\(logarithms\)
For
\(2^3 = 8\) is written as
\(log_2 8 = 3\)
And is read as: logarithm of
\(8\) to base
\(2\) is equal to
\(3\)
\begin{equation*}
a^b = c ⟺ log_a c = b
\end{equation*}
\(a^b = c\) represent the Index notation
\(log_a c = b\) represent the Logarithmic notation
Example 1.2.8 .
The table below contains numbers in
index form and
logarithm form . Fill and complete the table.
Table 1.2.9.
Exponential Form Logarithmic Form
__
\(\log_2 32 = 5\)
\(10^4 = 10,000\) __
\(3^3 = 27\) __
\(5^2 = 25\) __
__
\(\log_7 7 = 1\)
__
\(\log_4 64 = 3\)
Example 1.2.10 .
What is the logarithmic form of the following exponents:
When
\(6^2 = 36\) then,
\(\log_6 36 = 2\)
When
\(9^3 = 729\) then,
\(\log_9 729 = 3\)
When
\(4^5 = 1024\) then,
\(\log_4 1024 = 5\)
Exercises Exercises
1. What are the logarithmic form of:
\(\displaystyle 2^6 = 64 \qquad \qquad \qquad \qquad \text{e)}\,\,8^4 = 4096 \)
\(\displaystyle 5^3 = 125 \qquad \qquad \qquad \qquad \text{f)}\,\, 6^y = 216\)
\(\displaystyle 3^x = 81 \qquad \qquad \qquad \qquad \text{g)}\,\, 9^{\frac {1}{2}} = 3\)
\(\displaystyle 8^{\frac {2}{3}} = 4 \qquad \qquad \qquad \qquad \text{h)}\,\, 4^{-2} = \frac {1}{16}\)
2. Express
\(10^4 = 10000\) in logarithmic form.
3. Find the value of
\(y\) given that
\(\log_y 81 = 4\)
4. Solve for
\(x\) if
\(\log_2 x = 5\)
5. Convert
\(8^x = 512\) to logarithmic form and solve for
\(x\text{.}\)
Subsubsection 1.2.2.3 Determining Common Logarithms Using Mathematical Tables and Calculators
Common logarithms, also known as logarithms to base
\(10\text{,}\) are written as
\(\log x\) instead of
\(\log_{10} x\text{.}\)
When
\begin{equation*}
10 x = y
\end{equation*}
It means that
\(10\) must be raised to the power of
\(y\) to give
\(x\text{,}\) that is:
\begin{equation*}
10^y = x
\end{equation*}
For example: \(\log 100 = 2\) because
\(10^2 = 100\)
Common logarithms simplify complex multiplications, divisions, and exponentiation by converting them into easier operations using logarithmic laws.
In Grade
\(8\text{,}\) you learned how to use mathematical tables to find squares, square roots, and reciprocals of numbers. Here we will use the knowledge to reading tables of logarithm to base
\(10\text{.}\)
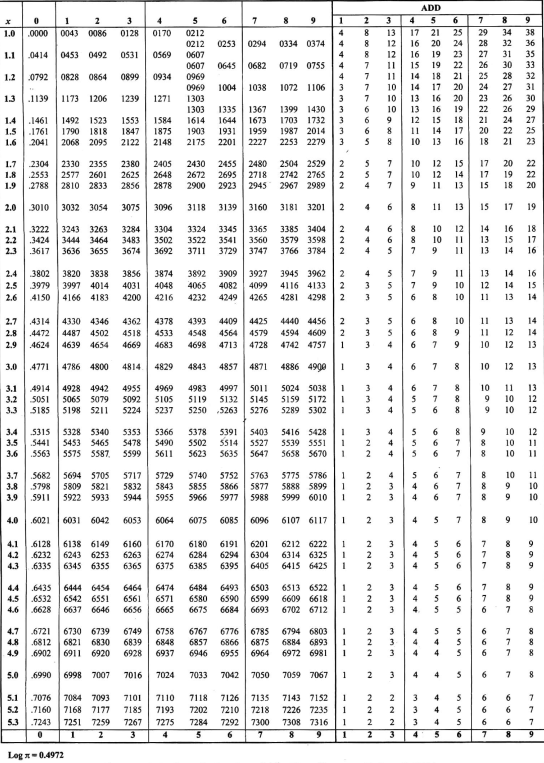
Here is an extract of a logarithm table to base
\(10\)
Positive Numbers greater than \(1\)
Example 1.2.12 .
Find
\(\log (472.8)\) using a logarithm table.
Solution .
Using a logarithm table, follow these steps:
Identify the characteristic:
Write
\(472.8\) in standard form
\begin{equation*}
\log (472.8) = \log (4.728 \times 10^2)
\end{equation*}
The characteristic is
\(2\) since
\(10^2 \leq 472.8 \lt 10^3\text{.}\)
Find the mantissa from the log table:
Locate
\(47\) in the first column and move to the column labeled
\(2\text{.}\)
Read the value:
\(0.6749\text{.}\)
\begin{equation*}
\log (472) = 0.6749
\end{equation*}
Apply the mean difference for
\(8\text{:}\)
From the table, the mean difference for
\(8\) is
\(0.0007\text{.}\)
Add this to the mantissa:
\begin{equation*}
0.6749 + 0.0007 = 0.6756
\end{equation*}
Combine with the characteristic
\begin{equation*}
\log (472.8) = 2.6756
\end{equation*}
Using a calculator, we can confirm that
\(\log (472.8) \approx 2.6756\text{,}\) matching the value obtained from the logarithm table.
Positive Numbers less than \(1\)
Example 1.2.13 .
Use logarithm tables to solve
\(\log 0.00534\)
Solution .
Since
\(0.00534\) cannot be read directly from the table, first we need to write it in standard form;
Standard form of
\begin{equation*}
0.00534 = 5.34 \times 10^{-3}
\end{equation*}
Here, the characteristic is
\(-3\) and the mantissa is the logarithm of
\(5.34\text{.}\)
Using the logarithm table:
Locate \(53\) in the first column.
Move to the column labeled \(4\text{.}\)
Read the value: \(\log(5.34) = 0.7272\text{.}\)
Now, apply the logarithm property:
\begin{equation*}
\log(0.00534) = \log(5.34) + \log(10^{-3})
\end{equation*}
Since
\(\log(10^{-3}) = -3\text{,}\) we substitute:
\begin{equation*}
\log(0.00534) = 0.7272 - 3
\end{equation*}
\begin{equation*}
= \bar{3}.7272
\end{equation*}
The bar over
\(3\) represents a negative characteristic.
\begin{equation*}
\therefore \log 0.00534 = \bar{3}.7272
\end{equation*}
Exercises Exercises
1. Express the following numbers in standard form.
\(\displaystyle 4820 \qquad \qquad \qquad \qquad \text{e)}\,\, 0.000485\)
\(\displaystyle 37.6 \qquad \qquad \qquad \qquad \text{f)}\,\, 91800\)
\(\displaystyle 672000 \qquad \qquad \qquad \qquad \text{g)}\,\, 5.27 \times 10^5\)
\(\displaystyle 321000 \qquad \qquad \qquad \qquad \text{h)}\,\, 0.000672\)
2. Use a logarithm table to find the logarithm of the following numbers:
\(\displaystyle 0.00893 \qquad \qquad \qquad \qquad \text{e)}\,\, 0.000245\)
\(\displaystyle 3140 \qquad \qquad \qquad \qquad \text{f)}\,\, 6.42 \times 10^3\)
\(\displaystyle 52.7 \qquad \qquad \qquad \qquad \text{g)}\,\, 78900\)
\(\displaystyle 0.000978\)
Activity 1.2.7 . Exploring Logarithms in Real-Life Applications.
At individual level, go explore how logarithms are used in different fields such as engineering, finance, and science.
Research and describe two real-life applications of logarithms. Present your findings to the class.
The pH scale in chemistry is based on logarithms. Given that pH is defined as
\(\text{pH} = -\log[H^+]\text{,}\) determine the pH of a solution where
\([H^+] = 3.2 \times 10^{-4}\text{.}\)
The Richter scale measures earthquake intensity using the formula
\(R = \log \left( \frac{I}{I_0} \right)\text{,}\) where
\(I\) is the intensity of the earthquake and
\(I_0\) is the reference intensity. If an earthquake is 1000 times more intense than the reference, what is its magnitude on the Richter scale?
Use logarithm tables to evaluate
\(\sqrt{ \frac{(6.28 \times 42.5)}{9.81} }\text{.}\)
A country’s population grows exponentially according to the formula
\(P = P_0 e^{rt}\text{,}\) where
\(P_0\) is the initial population,
\(r\) is the growth rate, and
\(t\) is time in years. Solve for
\(t\) if a population doubles in
\(10\) years at a growth rate of
\(5\%\) per year.
The antilogarithm (antilog) of a number is the inverse operation of taking a logarithm. If
\(\log x = y\text{,}\) then
\(x\) is the antilog of
\(y\text{.}\) This means:
\begin{equation*}
x = 10^y
\end{equation*}
To find the antilogarithm of a number, we use logarithm tables or a calculator.
Finding Antilogarithms Using Logarithm Tables
To find the antilogarithm of a given logarithmic value using a logarithm table, follow these steps:
Separate the characteristic and mantissa.
Use the logarithm table to find the antilog of the mantissa.
Apply the characteristic as a power of 10.
Example 1.2.14 .
Find the antilogarithm of
\(2.6756\) using logarithm tables.
Solution .
Separate the characteristic and mantissa
\begin{equation*}
2.6756 = 2 + 0.6756
\end{equation*}
Find the antilogarithm of
\(0.6756\) using tables:
\begin{equation*}
\text{Antilog } (0.6756) = 4.735
\end{equation*}
Apply the characteristic:
\begin{equation*}
10^2 \times 4.735 = 473.5
\end{equation*}
Thus, the antilogarithm of
\(2.6756\) is
\(473.5\text{.}\)
Finding Antilogarithms Using a Calculator
When using a calculator, simply input the given logarithm value and use the inverse logarithm function:
\begin{equation*}
x = 10^y
\end{equation*}
For example, to find
\(\text{Antilog } (1.3562)\) on a calculator:
Press
10^x or
INV +
LOG and enter
\(1.3562\text{.}\)
Exercises Exercises
1. Find the antilogarithms of the following logarithmic values using logarithm tables:
\(\displaystyle \log P = 1.3562\)
\(\displaystyle \log Q = 3.4821\)
\(\displaystyle \log R = 0.7294\)
\(\displaystyle \log S = 4.2187\)
2. Solve the following logarithms using a calculator:
\(\displaystyle \log a = 2.1457\)
\(\displaystyle \log b = 0.8743\)
\(\displaystyle \log c = 3.5961\)
\(\displaystyle \log d = 1.9999\)
Subsubsection 1.2.2.4 Multiplying and Dividing Logarithms
Logarithms simplify multiplication and division by converting them into addition and subtraction, respectively. This is particularly useful when dealing with large numbers.
Example 1.2.15 .
Find
\(236.5 \times 42.8\) using logarithm table.
Solution .
Find the logarithm of each number from the logarithm table:
\begin{equation*}
\log 236.5 = 2.3741, \quad \log 42.8 = 1.6318
\end{equation*}
\begin{equation*}
2.3741 + 1.6318 = 4.0059
\end{equation*}
Find the antilogarithm of
\(4.0059\text{:}\)
\begin{equation*}
\text{Antilog} (4.0059) \approx 10160
\end{equation*}
Thus,
\(236.5 \times 42.8 \approx 10160\text{.}\)
Example 1.2.16 .
Find
\(\frac{528.6}{24.7}\) using logarithm tables.
Solution .
Find the logarithm of each number from the logarithm table:
\begin{equation*}
\log 528.6 = 2.7233, \quad \log 24.7 = 1.3927
\end{equation*}
\begin{equation*}
2.7233 - 1.3927 = 1.3306
\end{equation*}
Find the antilogarithm of
\(1.3306\text{:}\)
\begin{equation*}
\text{Antilog} (1.3306) \approx 21.4
\end{equation*}
Thus,
\(\frac{528.6}{24.7} \approx 21.4\text{.}\)
Subsubsection 1.2.2.5 Applying Logarithms to Powers and Roots
Logarithms can be used to simplify calculations involving powers and roots by converting exponentiation into multiplication and roots into division.
Activity 1.2.8 .
Use your calculator and math reasoning to solve the following expressions involving logarithms:
\begin{equation*}
\log(10000)
\end{equation*}
Now rewrite
\(10000\) as a power of
\(10\text{:}\)
\begin{equation*}
\log(10000) = \log(10^4)
\end{equation*}
Apply the logarithmic law:
\begin{equation*}
\log(a^b) = b \times \log(a)
\end{equation*}
\begin{equation*}
\log(10^4) = 4 \times \log(10)
\end{equation*}
\begin{equation*}
= 4 \times 1 = 4
\end{equation*}
\begin{equation*}
\log(100)
\end{equation*}
\begin{equation*}
\log(1000000)
\end{equation*}
\begin{equation*}
\log(\sqrt{100})
\end{equation*}
\begin{equation*}
\log(\sqrt[3]{1000})
\end{equation*}
What do you observe when applying logarithms to square and cube roots?
Why does
\begin{equation*}
\log(\sqrt{100})
\end{equation*}
give half of
\begin{equation*}
\log(100)\text{?}
\end{equation*}
What general rule can you form for logarithms and powers?
Logarithms help simplify calculations involving powers and roots.
For example:
\(\log(a^b) = b \times \log(a)\text{,}\) and
\(\log(\sqrt{a}) = \frac{1}{2} \times \log(a)\text{.}\)
Example 1.2.17 .
Evaluate
\((23.5)^4\) using logarithm tables.
Solution .
Find the logarithm of
\(23.5\) from the logarithm table:
\begin{equation*}
\log 23.5 = 1.3711
\end{equation*}
Multiply by the exponent
\(4\text{:}\)
\begin{equation*}
1.3711 \times 4 = 5.4844
\end{equation*}
Find the antilogarithm of
\(5.4844\text{:}\)
\begin{equation*}
\text{Antilog} (5.4844) \approx 304000
\end{equation*}
Thus,
\((23.5)^4 \approx 304000\text{.}\)
Example 1.2.18 .
Evaluate
\(\sqrt[3]{524.8}\) using logarithm tables.
Solution .
Find the logarithm of
\(524.8\) from the logarithm table:
\begin{equation*}
\log 524.8 = 2.7200
\end{equation*}
Divide the logarithm by
\(3\) (since it is a cube root):
\begin{equation*}
\frac{2.7200}{3} = 0.9067
\end{equation*}
Find the antilogarithm of
\(0.9067\text{:}\)
\begin{equation*}
\text{Antilog} (0.9067) \approx 8.1
\end{equation*}
Thus,
\(\sqrt[3]{524.8} \approx 8.1\text{.}\)
Exercises Exercises
1. Use logarithm tables to evaluate the following:
\(\displaystyle 345.6 \times 78.9\)
\(\displaystyle 6284 \times 92.5\)
\(\displaystyle 0.0482 \times 53.7\)
2. Use logarithms to calculate:
\(\displaystyle 652.3 \div 12.7\)
\(\displaystyle 0.0854 \div 3.42\)
\(\displaystyle 4312 \div 58.3\)
3. Solve the following using logarithms:
\(\displaystyle (78.5)^3\)
\(\displaystyle (254.6)^4\)
\(\displaystyle (12.75)^{2.5}\)
4. Compute the following roots using logarithms:
\(\displaystyle \sqrt[3]{658.4}\)
\(\displaystyle \sqrt{82.6}\)
\(\displaystyle \sqrt[4]{3126}\)
5. A square field has an area of
\(18432\) square metres. Use logarithms to determine the length of one side.
6. Use logarithm tables to evaluate:
\(\displaystyle \sqrt{ \frac{(4.56 \times 12.3)}{24.7} }\)
\(\displaystyle \sqrt{ \frac{(2.718 \times 9.81)}{5.432 \times 3.14} }\)
\(\displaystyle \frac{\sqrt{52.8 \times 24.6}}{\sqrt{31.5}}\)
\(\displaystyle \sqrt[3]{\frac{(6.75 \times 432)}{0.89}}\)
\(\displaystyle \sqrt[4]{\frac{(8462 \times 23.7)}{673}}\)
7. The volume of a cube is
\(79507\) cubic centimetres. Use logarithms to find the length of one side.
