Skip to main content

Grade 10 Mathematics Learners’ Book

INNODEMS

Subsection 1.2.2 Logarithms

Why Logarithms?

In the previous section, indices allowed us to simplify very large or small numbers by expressing them in terms of powers. However, there are situations where we need to reverse this process, rather than finding the result of a power, we need to determine the exponent itself. This is where logarithms come into play.
🔗
A \(logarithm\) is the inverse of an exponent (index). It tells us the power to which a specific base must be raised to produce a given number.
🔗
For example:
🔗
Exponent Form: \(2^3 = 8.\)
🔗
Logarithm Form: \(log_2 8 = 3.\)
🔗
In simpler terms, a \(logarithm\) answers the question: "To what power must the base be raised to produce a certain number?"
🔗
Why Are Logarithms Important?
🔗
Logarithms are crucial for solving equations involving exponents. They simplify computations and are widely used in fields like:
🔗
  • Finance: calculating compound interest or investment growth.
    🔗
    🔗
  • Science and Engineering: understanding radioactive decay, measuring sound intensity, or modeling population growth.
    🔗
    🔗
🔗

Subsubsection 1.2.2.1 Logarithms notation

Activity 1.2.5.

Work in groups: Form groups of \(2\) or \(3\) students
🔗
Materials: A Paper/book and a pen
🔗
Instructions:
🔗
Pick a number from the set: \(81, 243, 512\) or \(1000\)
🔗
Break down the chosen number into its prime factors.
🔗
Start by dividing the number by its smallest prime factor repeatedly until only prime factors remain.
🔗
e.g. \(8 = 2 \times 2 \times 2 = 2^3\)
🔗
Express your final result in index form
🔗
Reflect on how the indices relate to logarithms:
🔗
For example, \(2^3 =8\) translates to \(\log_2 8 = 3.\)
🔗
🔗
Key Takeaway:
🔗
Logarithms are simply another way of expressing indices. They bridge the gap between exponential and logarithmic notation:
🔗
  • Exponential Form: \(a^b = c.\)
    🔗
    Logarithmic Form:\(\log_a c = b.\)
    🔗
    🔗
🔗
\(e.g\)
\begin{equation*} 8 = 2 \times 2 \times 2 = 2^3 \end{equation*}
🔗
\begin{equation*} 4 = 2 \times 2 = 2^2 \end{equation*}
🔗
\begin{equation*} 2 = 2^1 \end{equation*}
🔗
The powers/ indices \(3, 2, 1\) are the \(logarithms\)
🔗
For \(2^3 = 8\) is written as \(log_2 8 = 3\)
🔗
And is read as: logarithm of \(8\) to base \(2\) is equal to \(3\)
🔗
The general form is:
🔗
\begin{equation*} a^b = c ⟺ log_a c = b \end{equation*}
🔗
\(a^b = c\) represent the Index notation
🔗
\(log_a c = b\) represent the Logarithmic notation
🔗

Example 1.2.19.

The table below contains numbers in index form and logarithm form. Fill and complete the table.
🔗
Table 1.2.20.
🔗
Exponential Form Logarithmic Form
__ \(\log_2 32 = 5\)
\(10^4 = 10,000\) __
\(3^3 = 27\) __
\(5^2 = 25\) __
__ \(\log_7 7 = 1\)
__ \(\log_4 64 = 3\)
🔗

Example 1.2.21.

What is the logarithmic form of the following exponents:
🔗
  1. \(6^2 = 36\)
    🔗
    When \(6^2 = 36\) then, \(\log_6 36 = 2\)
    🔗
    🔗
  2. \(9^3 = 729\)
    🔗
    When \(9^3 = 729\) then, \(\log_9 729 = 3\)
    🔗
    🔗
  3. \(4^5 = 1024\)
    🔗
    When \(4^5 = 1024\) then, \(\log_4 1024 = 5\)
    🔗
    🔗
🔗
🔗

Checkpoint 1.2.22. Compute Logs Base 10.

Load the question by clicking the button below.
🔗
🔗

Checkpoint 1.2.23. Expressing an Exponential Number in Logarithmic Form.

Load the question by clicking the button below.
🔗
🔗

Checkpoint 1.2.24. Rewrite Complex Exponential Relationship into Logarithmic Form.

Load the question by clicking the button below.
🔗
🔗

Exercises Exercises

1.
What are the logarithmic form of:
🔗
  1. \(\displaystyle 2^6 = 64 \qquad \qquad \qquad \qquad \text{e)}\,\,8^4 = 4096 \)
    🔗
    🔗
  2. \(\displaystyle 5^3 = 125 \qquad \qquad \qquad \qquad \text{f)}\,\, 6^y = 216\)
    🔗
    🔗
  3. \(\displaystyle 3^x = 81 \qquad \qquad \qquad \qquad \text{g)}\,\, 9^{\frac {1}{2}} = 3\)
    🔗
    🔗
  4. \(\displaystyle 8^{\frac {2}{3}} = 4 \qquad \qquad \qquad \qquad \text{h)}\,\, 4^{-2} = \frac {1}{16}\)
    🔗
    🔗
🔗
🔗
2.
Express \(10^4 = 10000\) in logarithmic form.
🔗
🔗
3.
Find the value of \(y\) given that \(\log_y 81 = 4\)
🔗
🔗
4.
Solve for \(x\) if \(\log_2 x = 5\)
🔗
🔗
5.
Convert \(8^x = 512\) to logarithmic form and solve for \(x\text{.}\)
🔗
🔗
🔗
🔗

Subsubsection 1.2.2.2 Using Logarithms with Standard Form

Standard form is a way of writing very large or very small numbers in a more manageable format. It is expressed as:
🔗
\begin{equation*} B \times 10^x \end{equation*}
🔗
Where:
🔗
  • \(B\) is a number between \(1\) and \(10\) \((1 \leq B \lt 100)\)
    🔗
    🔗
  • \(x\) is an integer (positive for large numbers and negative for small numbers)
    🔗
    🔗
🔗

Activity 1.2.6.

Work in groups: Form groups of \(2\) or \(3\) students
🔗
Instruction:
🔗
  1. Write any five digit number in your book
    🔗
    🔗
  2. Identify the first non-zero digit from the left.
    🔗
    🔗
  3. Place a decimal point after this digit.
    🔗
    🔗
  4. Count how many places the decimal has moved;
    🔗
    • If moved left, the exponent is positive.
      🔗
      🔗
    • If moved right, the exponent is negative.
      🔗
      🔗
    🔗
    🔗
  5. Express the number in the form \(B \times 10^x\)
    🔗
    🔗
🔗
🔗
Examples:
🔗
  • The distance from the Earth to the Sun is approximately \(149,600,000 \, km. \)
    🔗
    \begin{equation*} 149,600,000 = 1.496 \times 10^8 \, km \end{equation*}
    🔗
    🔗
  • The size of a red blood cell is about \(0.000007\) m
    🔗
    \begin{equation*} 0.000007 = 7.0 \times 10^{-6} m \end{equation*}
    🔗
    🔗
🔗
Further Activity:
🔗
  • The population of Kenya is approximately \(54,985,698\text{.}\) Express this number in standard form.
    🔗
    🔗
  • The size of a human hair is about \(0.00008\) metres. Express the length in standard form.
    🔗
    🔗
  • The charge of an electron is \(0.00000000000000000016\) coulombs. Convert this to standard form.
    🔗
    🔗
🔗
Finding Logarithms of Numbers in Standard Form:
🔗

Example 1.2.25.

Find \(\log (4.5 \times 10^5)\)
🔗
Solution.
\begin{equation*} \log (4.5 \times 10^5) = \log 4.5 \times 10^5 \end{equation*}
🔗
\begin{equation*} \log 4.5 = 0.6535 \end{equation*}
🔗
\begin{equation*} \therefore \log 450000 = 5.6535 \end{equation*}
🔗
🔗
🔗
In this case \(5\) is the characteristic. The characteristic is the whole number part of a logarithm. It tells us how large or small the number is based on powers of \(10\text{.}\)
🔗
\(0.6535\) is the mantissa. The mantissa is the decimal part of the logarithm, found using logarithm tables. It depends on the significant digits of the number but is always positive.
🔗
Key Takeaway:
🔗
  • For numbers greater than \(1\text{,}\) the characteristic is one less than the number of digits before the decimal point.
    🔗
    🔗
  • For numbers less than \(1\text{,}\) the characteristic is negative, often written in bar notation (e.g \(\overline{3}\) instead of \(-3\)).
    🔗
    🔗
🔗

Checkpoint 1.2.26. Using Logarithms with Standard Form.

Load the question by clicking the button below.
🔗
🔗

Checkpoint 1.2.27. Using Logarithms to Find the Power Part of Standard Form.

Load the question by clicking the button below.
🔗
🔗
🔗

Subsubsection 1.2.2.3 Determining Common Logarithms Using Mathematical Tables and Calculators

Common Logarithms
🔗
Common logarithms, also known as logarithms to base \(10\text{,}\) are written as \(\log x\) instead of \(\log_{10} x\text{.}\)
🔗
When
\begin{equation*} 10 x = y \end{equation*}
🔗
It means that \(10\) must be raised to the power of \(y\) to give \(x\text{,}\) that is:
🔗
\begin{equation*} 10^y = x \end{equation*}
🔗
For example: \(\log 100 = 2\) because \(10^2 = 100\)
🔗
Common logarithms simplify complex multiplications, divisions, and exponentiation by converting them into easier operations using logarithmic laws.
🔗
Using Logarithm Tables
🔗
In Grade \(8\text{,}\) you learned how to use mathematical tables to find squares, square roots, and reciprocals of numbers. Here we will use the mathematical tables to determine logarithms to base \(10\text{.}\)
🔗
Here is an extract of a logarithm table to base \(10\)
🔗
Logarithm table to base 10
Positive Numbers greater than \(1\)
🔗

Example 1.2.28.

  1. Find \(\log (472.8)\) using a logarithm table.
    🔗
    🔗
🔗
Solution.
Using a logarithm table, follow these steps:
🔗
  1. Identify the characteristic:
    🔗
    Write \(472.8\) in standard form
    🔗
    \begin{equation*} \log (472.8) = \log (4.728 \times 10^2) \end{equation*}
    🔗
    The characteristic is \(2\) since \(10^2 \leq 472.8 \lt 10^3\text{.}\)
    🔗
    🔗
  2. Find the mantissa from the log table:
    🔗
    Locate \(47\) in the first column and move to the column labeled \(2\text{.}\)
    🔗
    Read the value: \(0.6749\text{.}\)
    🔗
    \begin{equation*} \log (472) = 0.6749 \end{equation*}
    🔗
    🔗
  3. Apply the mean difference for \(8\text{:}\)
    🔗
    From the table, the mean difference for \(8\) is \(0.0007\text{.}\)
    🔗
    Add this to the mantissa:
    🔗
    \begin{equation*} 0.6749 + 0.0007 = 0.6756 \end{equation*}
    🔗
    🔗
  4. Combine with the characteristic
    🔗
    Therefore;
    🔗
    \begin{equation*} \log (472.8) = 2.6756 \end{equation*}
    🔗
    🔗
🔗
Using a calculator, we can confirm that \(\log (472.8) \approx 2.6756\text{,}\) matching the value obtained from the logarithm table.
🔗
🔗
🔗
Positive Numbers less than \(1\)
🔗

Example 1.2.29.

Use logarithm tables to solve \(\log 0.00534\)
🔗
Solution.
Since \(0.00534\) cannot be read directly from the table, first we need to write it in standard form;
🔗
Standard form of
\begin{equation*} 0.00534 = 5.34 \times 10^{-3} \end{equation*}
🔗
Here, the characteristic is \(-3\) and the mantissa is the logarithm of \(5.34\text{.}\)
🔗
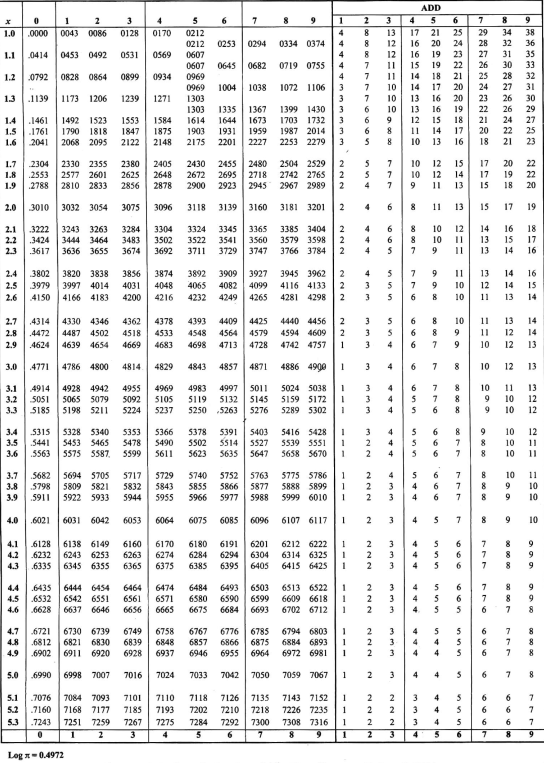
Using the logarithm table:
🔗
  • Locate \(53\) in the first column.
    🔗
  • Move to the column labeled \(4\text{.}\)
    🔗
  • Read the value: \(\log(5.34) = 0.7272\text{.}\)
    🔗
🔗
Now, apply the logarithm property:
🔗
\begin{equation*} \log(0.00534) = \log(5.34) + \log(10^{-3}) \end{equation*}
🔗
Since \(\log(10^{-3}) = -3\text{,}\) we substitute:
🔗
\begin{equation*} \log(0.00534) = 0.7272 - 3 \end{equation*}
🔗
\begin{equation*} = \bar{3}.7272 \end{equation*}
🔗
The bar over \(3\) represents a negative characteristic.
🔗
\begin{equation*} \therefore \log 0.00534 = \bar{3}.7272 \end{equation*}
🔗
🔗
🔗

Exercises Exercises

2.
Use a logarithm table to find the logarithm of the following numbers:
🔗
  1. \(\displaystyle 0.00893 \qquad \qquad \qquad \qquad \text{e)}\,\, 0.000245\)
    🔗
    🔗
  2. \(\displaystyle 3140 \qquad \qquad \qquad \qquad \text{f)}\,\, 6.42 \times 10^3\)
    🔗
    🔗
  3. \(\displaystyle 52.7 \qquad \qquad \qquad \qquad \text{g)}\,\, 78900\)
    🔗
    🔗
  4. \(\displaystyle 0.000978\)
    🔗
    🔗
🔗
🔗
🔗

Activity 1.2.7. Exploring Logarithms in Real-Life Applications.

At individual level, go explore how logarithms are used in different fields such as engineering, finance, and science.
🔗
  1. Research and describe two real-life applications of logarithms. Present your findings to the class.
    🔗
    🔗
  2. The pH scale in chemistry is based on logarithms. Given that pH is defined as \(\text{pH} = -\log[H^+]\text{,}\) determine the pH of a solution where \([H^+] = 3.2 \times 10^{-4}\text{.}\)
    🔗
    🔗
  3. The Richter scale measures earthquake intensity using the formula \(R = \log \left( \frac{I}{I_0} \right)\text{,}\) where \(I\) is the intensity of the earthquake and \(I_0\) is the reference intensity. If an earthquake is 1000 times more intense than the reference, what is its magnitude on the Richter scale?
    🔗
    🔗
  4. Use logarithm tables to evaluate \(\sqrt{ \frac{(6.28 \times 42.5)}{9.81} }\text{.}\)
    🔗
    🔗
  5. A country’s population grows exponentially according to the formula \(P = P_0 e^{rt}\text{,}\) where \(P_0\) is the initial population, \(r\) is the growth rate, and \(t\) is time in years. Solve for \(t\) if a population doubles in \(10\) years at a growth rate of \(5\%\) per year.
    🔗
    🔗
🔗
🔗
Antilogarithms
🔗
The antilogarithm (antilog) of a number is the inverse operation of taking a logarithm. If \(\log x = y\text{,}\) then \(x\) is the antilog of \(y\text{.}\) This means:
🔗
\begin{equation*} x = 10^y \end{equation*}
🔗
To find the antilogarithm of a number, we use logarithm tables or a calculator.
🔗
Finding Antilogarithms Using Logarithm Tables
🔗
To find the antilogarithm of a given logarithmic value using a logarithm table, follow these steps:
🔗
  • Separate the characteristic and mantissa.
    🔗
    🔗
  • Use the logarithm table to find the antilog of the mantissa.
    🔗
    🔗
  • Apply the characteristic as a power of 10.
    🔗
    🔗
🔗

Example 1.2.30.

Find the antilogarithm of \(2.6756\) using logarithm tables.
🔗
Solution.
Separate the characteristic and mantissa
🔗
\begin{equation*} 2.6756 = 2 + 0.6756 \end{equation*}
🔗
Find the antilogarithm of \(0.6756\) using tables:
🔗
\begin{equation*} \text{Antilog } (0.6756) = 4.735 \end{equation*}
🔗
Apply the characteristic:
🔗
\begin{equation*} 10^2 \times 4.735 = 473.5 \end{equation*}
🔗
Thus, the antilogarithm of \(2.6756\) is \(473.5\text{.}\)
🔗
🔗
🔗
Finding Antilogarithms Using a Calculator
🔗
When using a calculator, simply input the given logarithm value and use the inverse logarithm function:
🔗
\begin{equation*} x = 10^y \end{equation*}
🔗
For example, to find \(\text{Antilog } (1.3562)\) on a calculator:
🔗
  • Press 10^x or INV + LOG and enter \(1.3562\text{.}\)
    🔗
    🔗
  • Record the results
    🔗
    🔗
🔗

Checkpoint 1.2.31. Computing Simple Logarithms.

Load the question by clicking the button below.
🔗
🔗

Checkpoint 1.2.32. Determining Common Logarithms Using a Calculator.

Load the question by clicking the button below.
🔗
🔗

Exercises Exercises

1.
Find the antilogarithms of the following logarithmic values using logarithm tables:
🔗
  1. \(\displaystyle \log P = 1.3562\)
    🔗
    🔗
  2. \(\displaystyle \log Q = 3.4821\)
    🔗
    🔗
  3. \(\displaystyle \log R = 0.7294\)
    🔗
    🔗
  4. \(\displaystyle \log S = 4.2187\)
    🔗
    🔗
🔗
🔗
2.
Solve the following logarithms using a calculator:
🔗
  1. \(\displaystyle \log a = 2.1457\)
    🔗
    🔗
  2. \(\displaystyle \log b = 0.8743\)
    🔗
    🔗
  3. \(\displaystyle \log c = 3.5961\)
    🔗
    🔗
  4. \(\displaystyle \log d = 1.9999\)
    🔗
    🔗
🔗
🔗
🔗
🔗

Subsubsection 1.2.2.4 Multiplying and Dividing Logarithms

Logarithms simplify multiplication and division by converting them into addition and subtraction, respectively. This is particularly useful when dealing with large numbers.
🔗

Example 1.2.33.

Find \(236.5 \times 42.8\) using logarithm table.
🔗
Solution.
Find the logarithm of each number from the logarithm table:
🔗
\begin{equation*} \log 236.5 = 2.3741, \quad \log 42.8 = 1.6318 \end{equation*}
🔗
Add the logarithms:
🔗
\begin{equation*} 2.3741 + 1.6318 = 4.0059 \end{equation*}
🔗
Find the antilogarithm of \(4.0059\text{:}\)
🔗
\begin{equation*} \text{Antilog} (4.0059) \approx 10160 \end{equation*}
🔗
Thus, \(236.5 \times 42.8 \approx 10160\text{.}\)
🔗
🔗
🔗

Example 1.2.34.

Find \(\frac{528.6}{24.7}\) using logarithm tables.
🔗
Solution.
Find the logarithm of each number from the logarithm table:
🔗
\begin{equation*} \log 528.6 = 2.7233, \quad \log 24.7 = 1.3927 \end{equation*}
🔗
Subtract the logarithms:
🔗
\begin{equation*} 2.7233 - 1.3927 = 1.3306 \end{equation*}
🔗
Find the antilogarithm of \(1.3306\text{:}\)
🔗
\begin{equation*} \text{Antilog} (1.3306) \approx 21.4 \end{equation*}
🔗
Thus, \(\frac{528.6}{24.7} \approx 21.4\text{.}\)
🔗
🔗
🔗
🔗

Subsubsection 1.2.2.5 Applying Logarithms to Powers and Roots

Logarithms can be used to simplify calculations involving powers and roots by converting exponentiation into multiplication and roots into division.
🔗

Activity 1.2.8.

Material needed:
🔗
🔗
Instructions:
🔗
Use your calculator and math reasoning to solve the following expressions involving logarithms:
🔗
\begin{equation*} \log(10000) \end{equation*}
🔗
Now rewrite \(10000\) as a power of \(10\text{:}\)
🔗
\begin{equation*} \log(10000) = \log(10^4) \end{equation*}
🔗
Apply the logarithmic law:
\begin{equation*} \log(a^b) = b \times \log(a) \end{equation*}
🔗
\begin{equation*} \log(10^4) = 4 \times \log(10) \end{equation*}
🔗
\begin{equation*} = 4 \times 1 = 4 \end{equation*}
🔗
Try the following:
🔗
  • \begin{equation*} \log(100) \end{equation*}
    🔗
    🔗
  • \begin{equation*} \log(1000000) \end{equation*}
    🔗
    🔗
  • \begin{equation*} \log(\sqrt{100}) \end{equation*}
    🔗
    🔗
  • \begin{equation*} \log(\sqrt[3]{1000}) \end{equation*}
    🔗
    🔗
🔗
  • What do you observe when applying logarithms to square and cube roots?
    🔗
    🔗
  • Why does
    \begin{equation*} \log(\sqrt{100}) \end{equation*}
    give half of
    \begin{equation*} \log(100)\text{?} \end{equation*}
    🔗
    🔗
  • What general rule can you form for logarithms and powers?
    🔗
    🔗
🔗
Key Takeaway:
🔗
Logarithms help simplify calculations involving powers and roots.
🔗
For example: \(\log(a^b) = b \times \log(a)\text{,}\) and \(\log(\sqrt{a}) = \frac{1}{2} \times \log(a)\text{.}\)
🔗
🔗

Example 1.2.35.

Evaluate \((23.5)^4\) using logarithm tables.
🔗
Solution.
Find the logarithm of \(23.5\) from the logarithm table:
🔗
\begin{equation*} \log 23.5 = 1.3711 \end{equation*}
🔗
Multiply by the exponent \(4\text{:}\)
🔗
\begin{equation*} 1.3711 \times 4 = 5.4844 \end{equation*}
🔗
Find the antilogarithm of \(5.4844\text{:}\)
🔗
\begin{equation*} \text{Antilog} (5.4844) \approx 304000 \end{equation*}
🔗
Thus, \((23.5)^4 \approx 304000\text{.}\)
🔗
🔗
🔗

Example 1.2.36.

Evaluate \(\sqrt[3]{524.8}\) using logarithm tables.
🔗
Solution.
Find the logarithm of \(524.8\) from the logarithm table:
🔗
\begin{equation*} \log 524.8 = 2.7200 \end{equation*}
🔗
Divide the logarithm by \(3\) (since it is a cube root):
🔗
\begin{equation*} \frac{2.7200}{3} = 0.9067 \end{equation*}
🔗
Find the antilogarithm of \(0.9067\text{:}\)
🔗
\begin{equation*} \text{Antilog} (0.9067) \approx 8.1 \end{equation*}
🔗
Thus, \(\sqrt[3]{524.8} \approx 8.1\text{.}\)
🔗
🔗
🔗

Exercises Exercises

1.
Use logarithm tables to evaluate the following:
🔗
  1. \(\displaystyle 345.6 \times 78.9\)
    🔗
    🔗
  2. \(\displaystyle 6284 \times 92.5\)
    🔗
    🔗
  3. \(\displaystyle 0.0482 \times 53.7\)
    🔗
    🔗
🔗
🔗
4.
Compute the following roots using logarithms:
🔗
  1. \(\displaystyle \sqrt[3]{658.4}\)
    🔗
    🔗
  2. \(\displaystyle \sqrt{82.6}\)
    🔗
    🔗
  3. \(\displaystyle \sqrt[4]{3126}\)
    🔗
    🔗
🔗
🔗
5.
A square field has an area of \(18432\) square metres. Use logarithms to determine the length of one side.
🔗
🔗
6.
Use logarithm tables to evaluate:
🔗
  1. \(\displaystyle \sqrt{ \frac{(4.56 \times 12.3)}{24.7} }\)
    🔗
    🔗
  2. \(\displaystyle \sqrt{ \frac{(2.718 \times 9.81)}{5.432 \times 3.14} }\)
    🔗
    🔗
  3. \(\displaystyle \frac{\sqrt{52.8 \times 24.6}}{\sqrt{31.5}}\)
    🔗
    🔗
  4. \(\displaystyle \sqrt[3]{\frac{(6.75 \times 432)}{0.89}}\)
    🔗
    🔗
  5. \(\displaystyle \sqrt[4]{\frac{(8462 \times 23.7)}{673}}\)
    🔗
    🔗
🔗
🔗
7.
The volume of a cube is \(79507\) cubic centimetres. Use logarithms to find the length of one side.
🔗
🔗
🔗
🔗
🔗
PrevTopNext