Activity 2.7.3.
\(\textbf{Surface area of a Cuboid}\)
View the net of a cuboid in order to understand how to find the surface area of the cuboid.
Subsection 2.7.2 Surface area of a cuboid
Activity 2.7.4. Brick wall construction..
\(\textbf{Materials needed;}\)
♦ Small bricks
♦ Rulers
♦ Worksheets
🔹 In your group build up a cuboid wall by stacking similar small bricks to a desired height.
🔹 Add more columns and rows until the wall is entirely covered with bricks and it resembles a box.
🔹 Count the number of bricks that you used and record.
🔹 Calculate the surface area of the cuboid using the formula: \(2(\text{l} \times \text{w}) + 2(\text{l} \times \text{h}) + 2(\text{w} \times \text{h})\)
🔹 Compare their results. What do you notice? Share with your group members and discuss why builders need surface area e.g. for painting or tiling, building up walls and houses etc.
\(\textbf{Key Takeaway}\)
A cuboid is also called a rectangular Prism.
\(\textbf{Rectangular Prism;}\) It has a rectangle at its base. A cube is a rectangular prism with all sides of equal length.
The surface area of a cuboid is the total area of all six faces of the cuboid.
When learning about area, we calculated the surface area of a cuboid. Since the opposite faces of a cuboid are identical, the \(\textbf{surface area of a cuboid}\) can be calculated by finding the \(\textbf{area of each face}\) and \(\textbf{then adding them together}\text{.}\)
In this section, we will calculate the surface area of a cuboid from their nets.
Example 2.7.2.
Find the surface area of the following rectangular prism:
Solution.
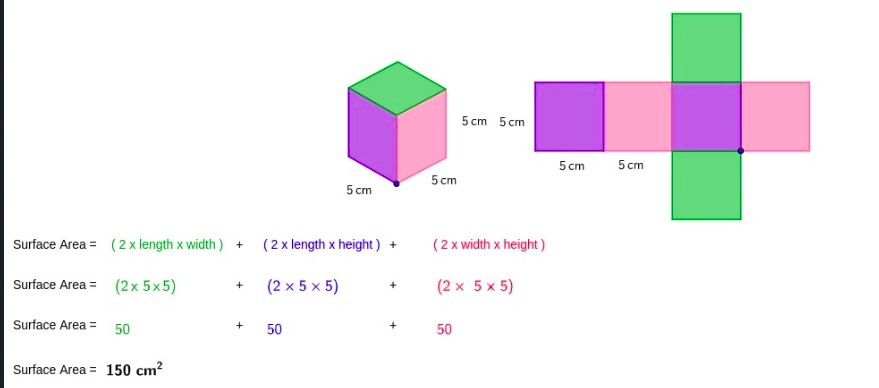
Sketch and label the net of the prism.
Find the areas of the different shapes in the ne
\begin{align*}
\text{large rectangle} = \amp \text{ perimeter of small rectangle} \times \text{length} \\
= \amp (3+8+3+8)\text{cm} \times 14\text{cm} \\
= \amp 22\text{cm} \times 14\text{cm} \\
= \amp 308\text{cm}^2
\end{align*}
\begin{align*}
2 \, \text{small rectangle} \amp = 2(8 \text{cm} \times 3\text{cm} ) \\
= \amp 2(18) \,\text{cm} \\
= \amp 36\text{cm}^2
\end{align*}
Find the sum of the areas of the faces
\begin{align*}
\text{large rectangle} + \text{small rectangle} = \amp (308 + 36)\text{cm}^2 \\
= \amp 344 \, \text{cm}^2
\end{align*}
The surface area of the rectangular prism is \(344 \, \text{cm}^2\)
\(\textbf{Exercise}\)
1. A rectangular cardboard box has dimensions of 10 cm by 8 cm by 5 cm. Calculate its total surface area, which represents the total material required to construct the box.
2. (a) A gift shop sells a rectangular gift box with dimensions 30 cm by 20 cm by 12 cm. If the shop owner wants to wrap the entire box, including all its faces, calculate the minimum amount of wrapping paper needed. If the wrapping paper is sold in rolls of 1 square meter, how many rolls would be needed to wrap 50 boxes?
(b) A gift box is being wrapped for a special occasion, and it has dimensions of 20 cm in length, 12 cm in width, and 10 cm in height. Calculate the exact amount of wrapping paper required to cover the entire box without any overlap.
3. A metal box used for shipping measures 25 cm by 15 cm by 10 cm. Compute the total amount of sheet metal required to construct the box, assuming no material is wasted.
4. The total surface area of a cuboid is given as 484 cm² and two of its dimensions are 8 cm and 6 cm. Determine the missing height (h) of the cuboid.
5. A cuboidal storage room has dimensions of 4 m by 5 m by 3 m. If the walls, floor and ceiling need to be painted, determine the total area that will be covered with paint.
6. A rectangular classroom has a length of 10 meters, a width of 8 meters and a height of 4 meters. The four walls and the ceiling need to be painted, but the floor is covered with tiles. If one litre of paint covers 5 square meters, calculate the total area to be painted and determine the amount of paint required.
7. A company is designing a cuboidal packaging box with dimensions 25 cm by 15 cm by 10 cm. The company wants to reduce costs by using the minimum possible material while ensuring the entire box is covered. Calculate the total surface area of the box and determine the cost of producing 1,000 such boxes if the material costs Ksh. 135 per square centimeter.
8. A swimming pool in the shape of a cuboid has dimensions 12 meters in length, 5 meters in width, and 3 meters in depth. The interior of the pool, including the bottom and the four walls, needs to be covered with waterproof tiles. If each tile has an area of 0.25 square meters, determine the total number of tiles required to completely cover the pool’s surface.
9. A metal storage container is shaped like a cuboid with dimensions 6 m by 4 m by 3 m. The container needs to be insulated on all its surfaces except for one of the 6 m by 4 m walls, which serves as the entrance. If the insulation material costs Ksh.295 per square meter, determine the total cost of insulating the container.
