Skip to main content

Grade 10 Mathematics Learners’ Book

INNODEMS

Subsection 1.1.4 Finding reciprocals of real numbers using mathematical tables and calculators

Mathematical tables and calculators provide alternative methods for quickly determining reciprocals, especially when dealing with large numbers or decimal values. In this section, we will explore how to use both tools effectively.
🔗

Subsubsection 1.1.4.1 Finding reciprocals of numbers using mathematical tables

Mathematical tables has reciprocal tables which are specially designed tables that allow you to quickly find the reciprocal of a number without doing any division. Each table lists a number along with its reciprocal, so you can look up the reciprocal directly.
🔗

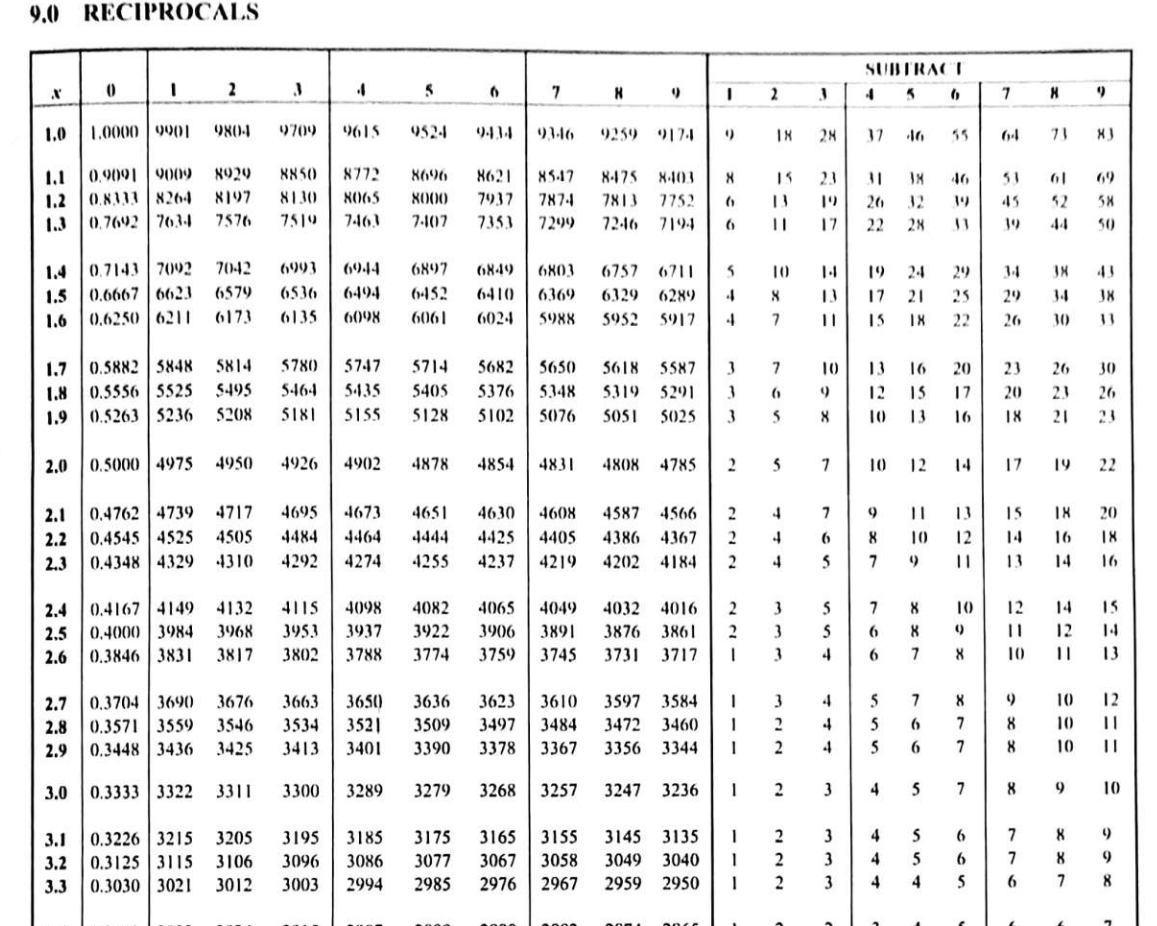
Activity 1.1.5.

\(\textbf{Each group should have a mathematical table}\)
🔗
1. Working in groups of \(5\text{,}\) consider the following numbers:
🔗
  1. \(\displaystyle \frac{3}{4}\)
    🔗
    🔗
  2. \(\displaystyle \frac{1}{3}\)
    🔗
    🔗
  3. \(\displaystyle 6\)
    🔗
    🔗
  4. \(\displaystyle 0.4167\)
    🔗
    🔗
🔗
2. Discuss how to use reciprocal tables to find reciprocals of each of the given numbers.
🔗
3. Determine the reciprocals of the numbers.
🔗
4. What did you realize?
🔗
5. Share your work with fellow learners.
🔗
🔗
\(\textbf{How to find reciprocals of numbers from the table.}\)
🔗
1. Given a large number e.g \(1252\text{,}\) express the number in standard form: \(1.252 \times 10^3\text{.}\) 1. Given a large number e.g \(1252\text{,}\) express the number in standard form: \(=1.252 \times 10^3\text{.}\)
🔗
2. Next, you find the reciprocal of the number from the reciprocal table as follows.
🔗
sample of the mathematical table
  1. Move down the column headed \(x\) to locate \(1.2\)
    🔗
    🔗
  2. Move to the right along the row that has \(1.2\) to the column headed \(5\text{.}\)
    🔗
    🔗
  3. Read the number at the intersection of the row and column which is \(0.8000\)
    🔗
    🔗
  4. Move farther to the right on the same row to the SUBTRACT column headed \(2\text{.}\)
    🔗
    🔗
  5. Read the number at the intersection of the row and column which is \(13\text{.}\)
    🔗
    🔗
  6. Subtract the number \(13\) from \(0.800\text{.}\) While subtracting align \(13\) to the right as shown below.
    🔗
    \(0\) \(.\) \(8\) \(0\) \(0\)
    - \(0\) \(.\) \(0\) \(1\) \(3\)
    \(0\) \(.\) \(7\) \(8\) \(7\)
    🔗
🔗
4. Calculate the reciprocal of \(10^3\text{.}\)
🔗
Since \(10^3\) can be written as \(1000\) then its reciprocal is \(\frac{1}{1000}\text{.}\)
🔗
5. Multiply \(0.787\) by \(\frac{1}{1000}\text{.}\)
🔗
6. Hence, the reciprocal of \(1252\) is given by \(0.787 \times \frac{1}{1000} = 0.000787\)
🔗

Example 1.1.15.

Use tables to find the reciprocal of \(0.154\text{.}\)
🔗
Solution.
Given \(0.154\text{,}\) first write it in standard form: \(1.54 \times 10^{-1}\text{.}\)
🔗
extract of mathematical table
Then, to locate the reciprocal of the given number:
🔗
  1. Move down the column headed \(x\) to locate \(1.5\text{.}\)
    🔗
    🔗
  2. Move to the right along the row that has \(1.5\) to the column headed \(4\text{.}\)
    🔗
    🔗
  3. Read the number at the intersection of the row and column which is \(0.6494\text{.}\)
    🔗
    🔗
🔗
Calculate the reciprocal of \(10^{-1}\text{.}\)
🔗
Since \(10^{-1}\) can be written as \(\frac{1}{10}\) then its reciprocal is \(\frac{10}{1} = 10\text{.}\)
🔗
Multiply \(0.6494\) by \(10\text{.}\)
🔗
The reciprocal of \(0.154\) is \(6.494\)
🔗
🔗
🔗

Example 1.1.16.

Murunga’s car consumes \(\frac{1}{8}\) liters of fuel per kilometer. Use tables to identify how far Murunga can drive with 1 liter?
🔗
Solution.
If \(\frac{1}{8} \text{liters} =1\)km,
🔗
Then \(1 \text{liter}= ?\) km
🔗
To find the distance Murunga drove using \(1\) liter, we first convert \(\frac{1}{8}\) to a decimal i.e \(1\div8 = 0.125\text{.}\)
🔗
Next, we write \(0.125\) in standard form: \(1.25 \times 10^{-1}\text{.}\)
🔗
extract of mathematical table
Move down the column headed \(x\) to locate \(1.2\text{.}\)
🔗
Move to the right along the row that has \(1.2\) to the column headed \(5\text{.}\)
🔗
Read the number at the intersection of the row and column which is \(0.8000\text{.}\)
🔗
Calculate the reciprocal of \(10^{-1}\text{.}\)
🔗
Since \(10^{-1}\) can be written as \(\frac{1}{10}\) then its reciprocal is \(\frac{10}{1} = 10\text{.}\)
🔗
Multiply \(0.8000\) by \(10\text{.}\)
🔗
\(0.8000 \times 10 = 8\)
🔗
Therefore, Murunga can drive \(8\) km using \(1\) l of fuel.
🔗
🔗
🔗
\(\textbf{Exercise}\)
🔗
1. Find the reciprocals of the following numbers using reciprocal tables:
🔗
  1. \(\displaystyle 4286\)
    🔗
    🔗
  2. \(\displaystyle 0.0458\)
    🔗
    🔗
  3. \(\displaystyle 0.007582\)
    🔗
    🔗
  4. \(\displaystyle 2.781\)
    🔗
    🔗
  5. \(\displaystyle \frac{3}{8}\)
    🔗
    🔗
  6. \(\displaystyle \frac{1}{0.1252} + \frac{1}{12.52}\)
    🔗
    🔗
  7. \(\displaystyle \frac{4}{0.648}\)
    🔗
    🔗
  8. \(\displaystyle \frac{6}{0.754} - \frac{1}{75.4}\)
    🔗
    🔗
🔗
2. Use mathematical tables to evaluate each of the following:
🔗
  1. \(\displaystyle \frac{100}{29.56}\)
    🔗
    🔗
  2. \(\displaystyle \frac{1}{\sqrt{0.2704}}\)
    🔗
    🔗
  3. \(\displaystyle \frac{1}{1.374^2}\)
    🔗
    🔗
  4. \(\displaystyle 1000 \times \frac{1}{0.7598}\)
    🔗
    🔗
  5. \(\displaystyle \frac{3}{\sqrt{2025}}\)
    🔗
    🔗
  6. \(\displaystyle 3.054^2 + \frac{1}{\sqrt {60.84}}\)
    🔗
    🔗
🔗
3. John measures that light takes \(0.000000455\) seconds to travel a certain distance. Given that frequency is defined as the reciprocal of time, calculate the frequency of the light using mathematical tables.
🔗
4. Maria conducted a survey to find out which games students enjoy. She discovered that \(0.6\) of the students preferred playing football. Use mathematical tables to find the reciprocal of \(0.6\text{.}\)
🔗
5. A farmer can plant \(0.85\) acres of land in one day. How many days will it take the farmer to plant one acre?(Hint: Use the reciprocal of the planting rate.)Use mathematical tables to find your answer.
🔗
6. John can type 80 words per minute.
  1. How many minutes does it take him to type one word?
    🔗
    🔗
  2. Based on your answer, how long will it take him to type a \(400\)-word essay?
    🔗
    🔗
🔗
7. A shopkeeper has \(96\) apples and packs them in groups of \(8\) apples per pack.
  1. How many packs does the shopkeeper make?
    🔗
    🔗
  2. What is the reciprocal of the number of packs?
    🔗
    🔗
🔗
🔗

Subsubsection 1.1.4.2 Finding reciprocals using a calculator

Activity 1.1.6.

1. Working in groups, use a calculator to work out the reciprocal of \(151.6\)
🔗
  1. Press the keys 1, ÷, 1 ,5 ,1, . ,6 in that order.
    🔗
    🔗
  2. Press the key =
    🔗
    🔗
🔗
2. Read the displayed result. What is the reciprocal of \(151.6\) from the calculator?
🔗
3. Work out the reciprocal of each of the following numbers using the calculator:
🔗
  1. \(\displaystyle 0.0038 \)
    🔗
    🔗
  2. \(\displaystyle 0.5498\)
    🔗
    🔗
  3. \(\displaystyle \frac{1}{8}\)
    🔗
    🔗
  4. \(\displaystyle 564\)
    🔗
    🔗
🔗
4. Discuss with other learners how you determine the reciprocal of a number using a calculator.
🔗
🔗
\(\textbf{Key Takeaway}\)
🔗
To find reciprocal of a number using a calculator:
🔗
  1. Enter the number into the calculator,
    🔗
    🔗
  2. Press the reciprocal button x⁻¹ or divide \(1\) by the number.
    🔗
    🔗
  3. Read the displayed result.
    🔗
    🔗
🔗
Example: To find the reciprocal of \(7\text{,}\)
🔗
  1. Press the key 1
    🔗
    🔗
  2. Press the key ÷
    🔗
    🔗
  3. Press the key 7
    🔗
    🔗
  4. Press the key =
    🔗
    🔗
🔗
Read the displayed result which is \(0.14285714286\text{.}\) Hence the reciprocal of \(7\) given to \(4\) decimal places is \(0.1429\text{.}\)
🔗

Example 1.1.17.

Find the reciprocal of the following using a calculator.
🔗
  1. \(\displaystyle 5.6\)
    🔗
    🔗
  2. \(\displaystyle 0.003\)
    🔗
    🔗
  3. \(\displaystyle 12.8\)
    🔗
    🔗
🔗
Solution.
i) To find the reciprocal of \(5.6\text{,}\) press the keys 1, ÷, 5, . then 6.
🔗
Press the key =
🔗
Read the reciprocal of \(5.6\) on the screen of the calculator.
🔗
Hence the reciprocal of \(5.6\) from the calculator is approximately \(0.1786\text{,}\) when rounded off to \(4\) decimal places.
🔗
ii) To calculate the reciprocal of \(0.003\) :
🔗
Press the keys 1,÷, 0, ., 0, 0, then 3.
🔗
Press the key =
🔗
Read the reciprocal of \(0.003\) on the screen of the calculator.
🔗
Therefore, the reciprocal of \(0.003\) from the calculator is: \(333.333333...\text{.}\) Also written as \(333.3333\) when rounded off to \(4\) decimal places.
🔗
iii) To calculate the reciprocal of \(12.8\text{:}\)
🔗
Press the keys 1, ÷, 1, 2, . then 8.
🔗
Press the key =
🔗
Read the reciprocal of \(12.8\) on the screen of the calculator.
🔗
Hence the reciprocal of \(12.8\) from the calculator is: \(0.078125\text{.}\)
🔗
🔗
🔗

Checkpoint 1.1.18. Using a Calculator to Find Reciprocals.

Load the question by clicking the button below.
🔗
🔗

Checkpoint 1.1.19. Finding Reciprocals of Rational and Irrational Numbers.

Load the question by clicking the button below.
🔗
🔗
\(\textbf{Exercise}\)
🔗
1. Find the reciprocal of the following numbers using a calculator:
🔗
  1. \(\displaystyle 8\)
    🔗
    🔗
  2. \(\displaystyle 125\)
    🔗
    🔗
  3. \(\displaystyle 598\)
    🔗
    🔗
  4. \(\displaystyle 8638\)
    🔗
    🔗
  5. \(\displaystyle 8.861\)
    🔗
    🔗
  6. \(\displaystyle 0.00067\)
    🔗
    🔗
  7. \(\displaystyle 0.01467\)
    🔗
    🔗
  8. \(\displaystyle 0.4875\)
    🔗
    🔗
🔗
2. A school cafeteria has \(8\) large trays of food to serve equally among the students. To find out how much food each student will get per tray, the cafeteria manager needs to calculate the reciprocal of \(8\text{.}\) Using a calculator, how can the manager find the reciprocal of \(8\text{,}\) and what is the answer?
🔗
3. A group of friends has \(5\) bottles of juice to share equally. Use a calculator to determine how much juice each person gets per bottle.
🔗
4. If a machine completes a task in \(6\) hours, its work rate per hour is the reciprocal of the time. Use a calculator to determine the reciprocal and explain what it represents.
🔗
5. A car travels \(12\) kilometers on \(1\) liter of fuel. Use a calculator to find out liters of fuel needed per kilometer.
🔗
6. Write down \(3\) numbers and work out their reciprocals using a calculator.
🔗
🔗
🔗
PrevTopNext