Skip to main content
Contents Dark Mode Prev Up Next \(\newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Subsection 2.4.5 Application of Trigonometric Ratios
In this section you will learn how trigonometry are used in real life situation and many more.
Subsubsection 2.4.5.1 Trigonometric Ratios to Angles of Elevation and Depression
Activity 2.4.10 .
\(\textbf{Work in groups}\)
Measuring tape or meter stick.
Protractor or paper tube.
Calculator (or table of trigonometric ratios).
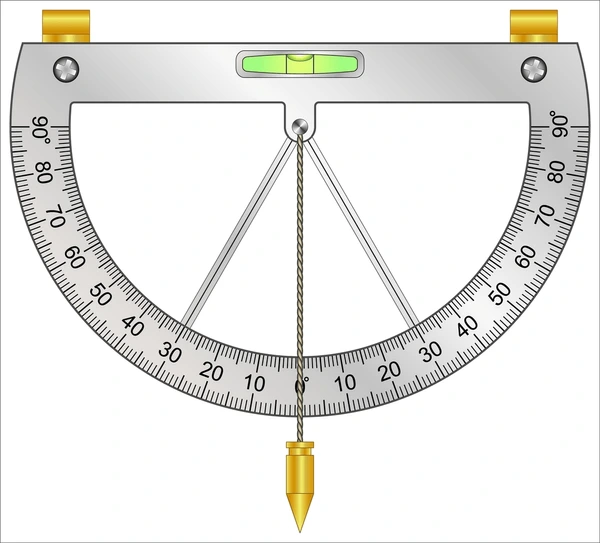
Use a clinometer, which is made from a string with a weight or rock attached, like the one shown below.
Find a tall object around your suraounding e.g tree, building, flagpole, etc.
Measure the distance from the base of the object to your position. Record this distance.
Use your clinometer to measure the angle of elevation from your eye level to the top of the object. Record the angle.
Draw a right triangle representing the situation. Label the distance you measured, the angle of elevation, and the unknown height of the object.
Decide which trigonometric ratio (sine, cosine, or tangent) you need to use to find the height.
Use the appropriate trigonometric ratio and the measured distance and angle to calculate the height of the object. Show your work
Write down your calculated height. Compare your result with your partner’s or other groups’ results. Discuss any differences.
\(\textbf{Extended Activity }\)
Activity 2.4.11 .
\(\textbf{Individual work}\)
What you require: Your homemade clinometer, a ruler or measuring tape, a notebook and pen and a friend (optional, but fun!)
Climb up to a higher place like a step, a balcony, or a small hill
Hold the clinometer at eye level, and look through it toward an object on the ground (like a cone, stone, or your friend’s shoes).
Watch the string and record the angle where it crosses the scale. That’s your angle of depression!
Measure the height from your eyes to the ground (that’s your vertical distance).
Calculate how far the object is from the base of your standing point.
Share and discuss your work with your classmates.
\(\textbf{Key Takeaway}\)
A
\(\textbf{clinometer}\) (or inclinometer) is a tool used to measure the angle of elevation (looking up) and the angle of depression (looking down).
The figure below shows a person standing on the ground, looking at an object at the top. This forms an angle of elevation. When looking down from a higher point, it forms an angle of depression.
The dashed line is the horizontal line.
\(\textbf{Angle of Elevation:}\) The angle measured upward from a horizontal line to an object above.
\(\textbf{Angle of Depression:}\) The angle measured downward from a horizontal line to an object below.
Example 2.4.31 .
A person stands
\(20\,m\) away from a tree. The angle of elevation from their eyes is (
\(1.6m\) above the ground) to the top of the tree is
\(35^\circ\text{.}\) Find the height of the tree.
Solution .
Look at the scetch below;
\begin{align*}
tan\,35^\circ=\amp \frac{\text{Tree height}-1.6 \,m}{20\,m} \\
\text{Tree height}=\amp (20 \times tan\,35^\circ)+1.6 \\
=\amp(20 \times 0.7002)+1.6 \\
=\amp 14+1.6 \\
= \amp 15.6\,m
\end{align*}
Example 2.4.32 .
A lighthouse is
\(50\,m \) tall. A sailor spots the top of the lighthouse at an angle of elevation of
\(^\circ\text{.}\) How far is the ship from the base of the lighthouse?
Solution .
Look at the scetch below;
\begin{align*}
tan\,25^\circ=\amp \frac{50\,m}{\text{Base}} \\
\text{Base}=\amp \frac{50}{tan\,25^\circ} \\
= \amp \frac{50}{0.4663} \\
=\amp 107.2\,m
\end{align*}
Example 2.4.33 .
A hiker stands on top of a hill that is
\(120\,cm\) high and looks down at a cabin in a valley. The angle of depression to the cabin is
\(40^\circ\text{.}\) Calculate the horizontal distance from the hiker to the cabin.
Solution .
\begin{align*}
tan\,40^\circ=\amp \frac{120\,cm}{\text{Cabin distance}} \\
\text{Cabin distance}=\amp \frac{120}{tan\,40^\circ} \\
=\amp \frac{120}{0.8391} \\
=\amp 143\,cm
\end{align*}
A ladder is leaning against a wall, forming an angle of
\(60^\circ\) with the ground. If the ladder is
\(10\,\) meters long, how high does it reach on the wall? Draw a right-angled triangle to represent the situation
If the angle of elevation is
\(30^\circ\) and the distance to the object is
\(50\,m\text{,}\) then the height above eye level is:
A drone flies to a height of
\(80\) meters above the ground. The angle of depression from the drone to a person standing on the ground is
\(30^\circ\text{.}\) Find the horizontal distance between the person and the drone’s projection on the ground. Sketch the problem.
A surveyor is standing
\(50\) meters away from the base of a mountain. The angle of elevation to the peak of the mountain is
\(30^\circ\text{.}\) Calculate the height of the mountain above the surveyor’s eye level.
If the angle of depression is
\(40^\circ\) and the horizontal distance to the object is
\(20\,m\text{,}\) the vertical top is:
\(\textbf{Technology Integration: Exploring Trigonometric Ratios}\)
To learn more on trigonometric ratios, find these interactive and insightful resources:
Khan Academy – Interactive Learning
Learn trigonometric ratios in right triangles through step-by-step tutorials and hands-on exercises.
Trigonometry Short Course Guide
A well-structured PDF with in-depth explanations and examples to strengthen your grasp of trigonometry.
YouTube Video – Visual Explanation
Gain a clear and concise understanding of trigonometric ratios with this engaging video tutorial.