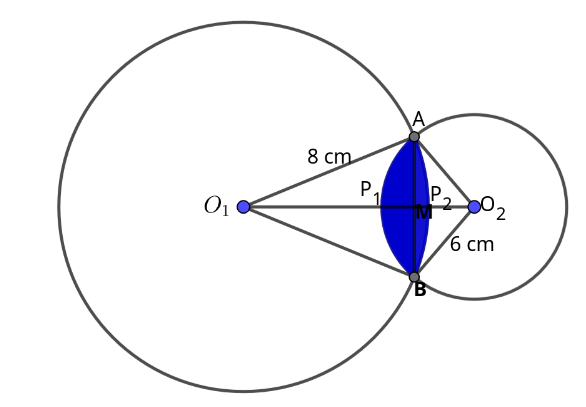
From
\(\triangle AO_1M\text{;}\)
\begin{align*}
O_1M=\amp \sqrt{8^2-4.5^2} \\
= \amp \sqrt{43.75} \\
=\amp 6.14\,cm
\end{align*}
From
\(\triangle AO_2M\text{;}\)
\begin{align*}
O_2M=\amp \sqrt{6^2-4.5^2} \\
= \amp \sqrt{15.75} \\
=\amp 3.969\,cm
\end{align*}
The area of the shaded region is the sum of the areas of segments
\(AP_1B\) and
\(AP_2B\text{.}\) \(\text{Area of segment }AP_1B = \text{area of
sector }C_2AP_1B – \text{area of }\triangle O_2AB.\)
\begin{align*}
\angle AO_2M=\amp\frac{AM}{AO_2} \\
=\amp \frac{4.5}{6} \\
=\amp 0.75 \\
\angle =\amp sin^{-1} \,(0.75) \\
= \amp 48.59^\circ
\end{align*}
\begin{align*}
\angle AO_2B=\amp 2\angle AO_2M\\
=\amp 2 \times 48.59^\circ \\
=\amp 97.18^\circ
\end{align*}
Area of segment
\(AP_1B\)
\begin{align*}
= \amp \frac{97.18}{360} \times 3.142 \times 6^2\\
=\amp 30.53
\end{align*}
Area of triangle.
\begin{align*}
=\amp\frac{1}{2} \times 9 \times 3.969 \\
=\amp 17.86
\end{align*}
\begin{align*}
\text{Area of segment}AP_1B=\amp 30.53 -17.86\\
=\amp 12.67\,cm^2
\end{align*}
\(\text{Area of segment }AP_2B = \text{area of
sector }0_1AP_2B – \text{area of }\triangle O_1AB.\)
\begin{align*}
\angle AO_1M=\amp\frac{AM}{AO_1} \\
=\amp \frac{4.5}{8} \\
=\amp 0.5625 \\
\angle =\amp sin^{-1} \,(0.5625) \\
= \amp 34.23^\circ
\end{align*}
\begin{align*}
\angle AO_1B=\amp 2\angle AO_1M\\
=\amp 2 \times 34.23^\circ \\
=\amp 68.46^\circ
\end{align*}
Area of segment
\(AP_2B\)
\begin{align*}
= \amp \frac{68.46}{360} \times 3.142 \times 8^2\\
=\amp 38.24
\end{align*}
Area of triangle.
\begin{align*}
=\amp\frac{1}{2} \times 9 \times 6.614 \\
=\amp 29.76
\end{align*}
\begin{align*}
\text{Area of segment}AP_2B=\amp 38.24-29.76\\
=\amp 8.48\,cm^2
\end{align*}
Therefore, area of the shaded region is given by;
\(\text{Area of segment}AP_1B+\text{Area of segment}AP_2B\)
\begin{align*}
=\amp 12.67\,cm^2+8.48\,cm^2\\
=\amp 21.15\,cm^2
\end{align*}