Enlargement

Subsection 2.1.2 Enlargement

Activity 2.1.2.

Work in pairs

🔗

(a)

Draw and label the \(x\) axis and \(y\) axis on the graph paper.

🔗

(b)

Mark the origin at \((0,0)\) and label it as \(\textbf{O}\text{.}\)

🔗

(c)

Plot the points \(A(2,3)\text{,}\) \(B(1,1)\text{,}\) and \(C(4,1)\text{.}\)

🔗

(d)

Connect points \(A\text{,}\) \(B\text{,}\) and \(C\) with straight lines to form triangle \(ABC\text{.}\)

🔗

(e)

Draw straight lines from O to \(A\text{,}\) \(O\) to \(B\text{,}\) and \(O\) to \(C\text{.}\)

🔗

(f)

Measure and record the lengths of \(OA\text{,}\) \(OB\text{,}\) and \(OC\text{.}\)

🔗

(g)

Extend each line to twice its original length and mark the new points as \(A'\text{,}\) \(B'\text{,}\) and \(C'\text{.}\)

🔗

(h)

Connect \(A'\text{,}\) \(B'\text{,}\) and \(C'\) to form the enlarged triangle \(A'B'C'\text{.}\)

🔗

(i)

Compare the two triangles and note any similarities.

🔗

(j)

Calculate the ratios \(\frac{OA'}{OA}\text{,}\) \(\frac{OB'}{OB}\text{,}\) and \(\frac{OC'}{OC}\text{,}\) what do you notice between the three ratios.

🔗

(k)

Discuss your findings with the rest of the class.

🔗

\(\textbf{Key Takeaway}\)

🔗

The process of obtaining triangle \(A'B'C'\) from triangle \(ABC\) is known as \(\textbf{enlargement.}\)
🔗

🔗
Triangle \(ABC\) is said to be object and triangle \(A'B'C'\text{,}\) its image under enlargement.The point \(O\) is known as the \(\textbf{centre of enlargement.}\)
🔗

🔗
To determine the scale factor, divide the length of the enlarged image by the corresponding length of the original object.
🔗

🔗

🔗

\begin{equation*} \frac{OA'}{OA} = \frac{OB'}{OB} = \frac{OC'}{OC} \end{equation*}

🔗

\begin{equation*} \frac{A'B'}{AB} = \frac{A'C'}{AC} = \frac{B'C'}{BC} \end{equation*}

🔗

Enlargement is a transformation that increases the size of a shape. The shape is enlarged by a scale factor. The scale factor is used to multiply the length of each side of the shape to get the length of the corresponding side of the enlarged shape.
🔗

🔗
In an enlargement, the object and its image remain similar. The linear scale factor of the enlargement determines the proportional transformation.
🔗

🔗
Lines connecting object points to their corresponding image points intersect at the center of enlargement. This property helps in determining the center of enlargement when both the object and its image are given.
🔗

🔗

🔗

Example 2.1.9.

🔗

In the figure below, Triangle \(P'Q'R'\) is the enlarged image of triangle \(PQR\text{,}\) with center \(O\)

🔗

(a) Given that \(OP=6\) \(cm\) and \(PP'=9\) \(cm\text{,}\) determine the linear scale factor of the enlargement.

🔗

(b) If \(QR=4\) \(cm\text{,}\) find the length of \(Q'R'\)

🔗

Figure 2.1.10.

🔗

Solution.

\begin{align*} \text {(a). Linear scale factor is:} \amp \\ \frac {OP'}{OP} =\amp \frac{(6+9)}{6}\\ = \amp \frac{15}{6}\\ = \amp \frac {5}{2} \end{align*}

🔗

\begin{align*} \text {(b).Linear scale factor } =\amp \frac {Q'R'}{QR}\\ \text {But QR} =\amp 4\, cm \\ \text {Therefore,} \frac {Q'R'}{QR}= \amp \frac {5}{2}\\ Q'P' =\amp \frac{(4 \times 5)}{2} \\ = \amp \frac{20}{2}\\ Q'P' = \amp 10\, cm \end{align*}

🔗

Example 2.1.11.

🔗

Construct any triangle \(XYZ\) and choose a point \(O\) outside the triangle. Using \(O\) as the center of enlargement and a scale factor of \(4\text{,}\) construct the enlarged image of triangle \(XYZ\) under the enlargement.

Solution.

Figure 2.1.12.

By measurement;

\(OX=1.8\) \(cm\text{,}\) \(OY=3.2\) \(cm\) and \(OZ=2.7\) \(cm\text{.}\)

🔗

\begin{align*} \text{To determine X', the image of X, We follow these steps:} \amp \\ OX= \amp 1.8\, cm\\ \frac {OX'}{OX}= \amp \text{scale factor}\\ \frac{OX'}{1.8} =4\amp \\ OX'= \amp 4 \times 1.8\, cm\\ = \amp 7.2\, cm \end{align*}

🔗

Extend \(OX\) and measure \(7.2\) \(cm\) from \(O\) to get \(X'\text{.}\)

🔗

\begin{align*} \text{To determine Y', the image of Y, We follow these steps:} \amp \\ OY= \amp 3.2\, cm\\ \frac {OY'}{OY}= \amp \text{scale factor}\\ \frac{OY'}{3.2} =4\amp \\ OX'= \amp 4 \times 3.2\, cm\\ = \amp 12.8\, cm \end{align*}

🔗

Extend \(OY\) and measure \(12.8\) \(cm\) from \(O\) to get \(Y'\text{.}\)

🔗

\begin{align*} \text{To determine Z', the image of Z, We follow these steps:} \amp \\ OZ= \amp 2.7\, cm\\ \frac {OZ'}{OZ}= \amp \text{scale factor}\\ \frac{OZ'}{2.7} =4\amp \\ OX'= \amp 4 \times 2.7\, cm\\ = \amp 10.8\, cm \end{align*}

🔗

Extend \(OZ\) and measure \(10.8\) \(cm\) from \(O\) to get \(Z'\text{.}\)

🔗

Example 2.1.13.

🔗

Triangle \(A'B'C'\) is the image of triangle \(ABC\) under an enlargement.Locate the centre of the enlargement.

🔗

Solution.

To locate the centre of enlargement we follow the following steps:

🔗

Draw lines connecting point \(A\) to \(A'\text{,}\) \(B\) to \(B'\) and \(C\) to \(C'\) and extend those lines. The intersection point of those lines, will be the center of enlargement.

🔗

Example 2.1.14.

🔗

Given that \(A\, (6,8)\text{,}\) \(B\, (8,8)\text{,}\) \(C\, (12,8)\text{,}\) \(D\, (14,2)\) and \(E\, (10,0)\) are the Vertices of the pentagon, find the vertices of its image after an enlargement with origin as the centre and scale factor of:

🔗

(a) \(2\)

🔗

(b) \(\frac{1}{2}\)

🔗

Solution.

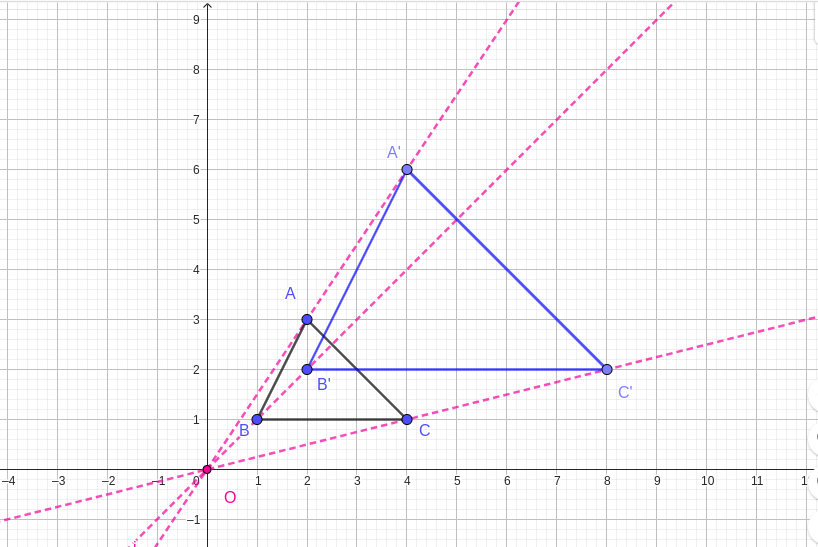
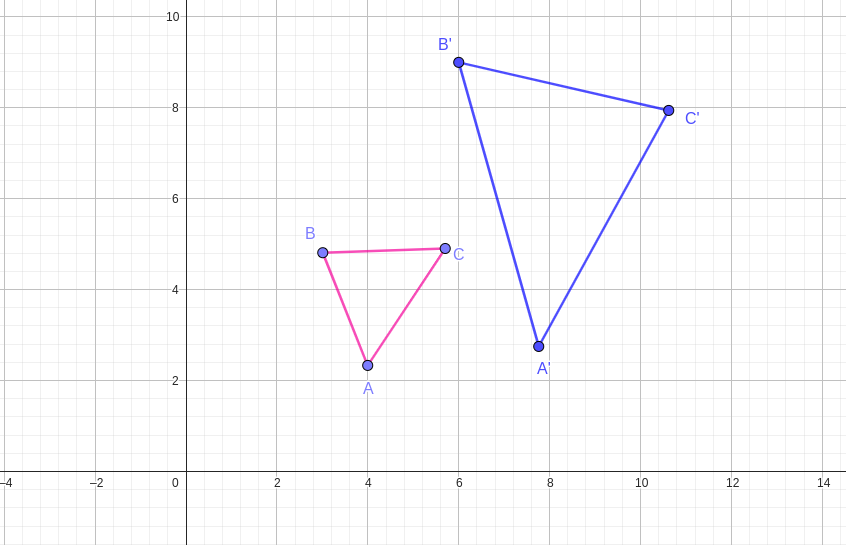
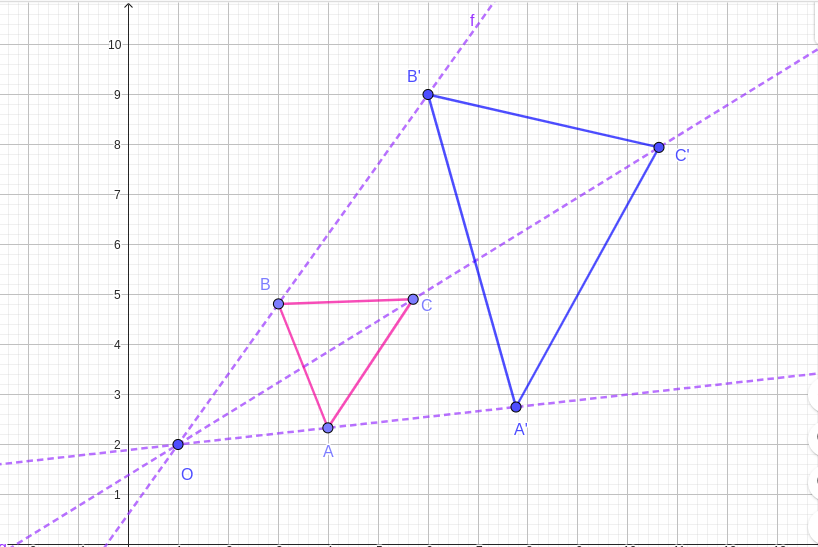
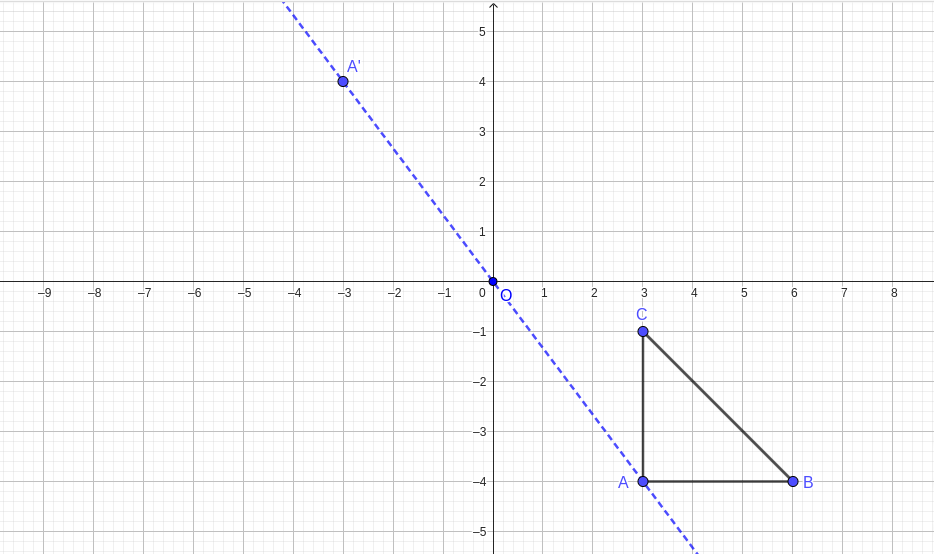
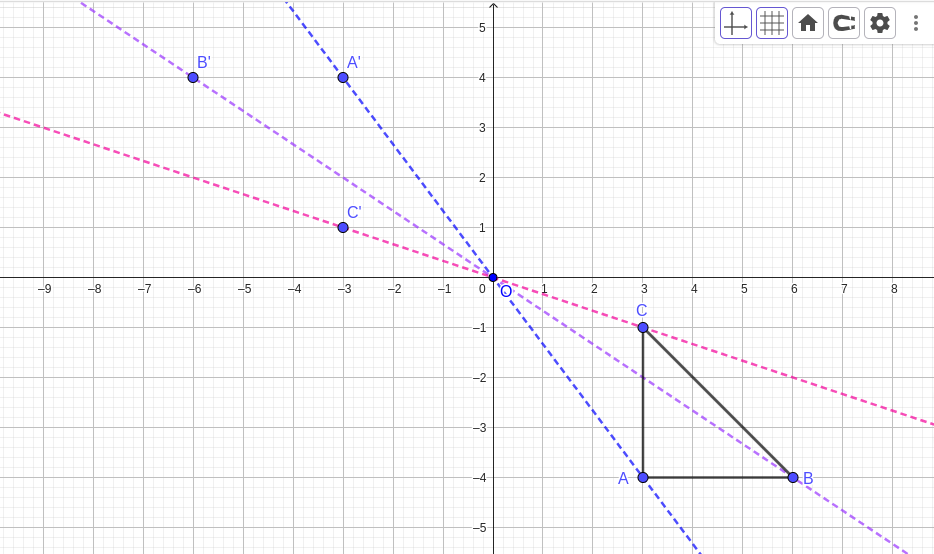
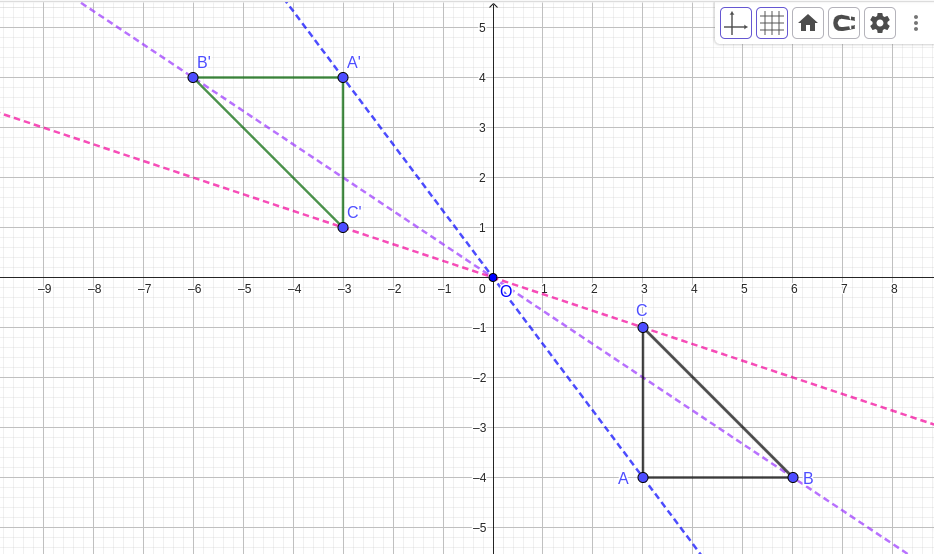
Given the centre of enlargement is \((0,0)\) and the scale factor \(k\text{,}\)We find the coordinates of the image as follows;

🔗

\((x',y')=\) \((kx,ky)\)

🔗

Applying this to the given co-odinates we get;

🔗

(a) for a scale factor of \(2\)

🔗

\begin{align*} A'=\amp(2\times 6), (2 \times 8)=(12,16) \\ B'=\amp(2\times 8), (2 \times 8)=(16,16) \\ C'=\amp(2\times 12), (2 \times 2)=(24,16) \\ D'=\amp(2\times 14), (2 \times 8)=(28,4) \\ E'=\amp(2\times 10), (2 \times 0)=(20,0) \\ \text{Vertices of the image}= \amp A' (12,16), B'(16,16), C' (24,16), D' (28,4) \text{and} E' (20,0) \end{align*}

🔗

(b) for a scale factor of \(\frac{1}{2}\)

🔗

\begin{align*} A'=\amp(\frac{1}{2}\times 6), (\frac{1}{2} \times 8)=(3,4) \\ B'=\amp(\frac{1}{2}\times 8), (\frac{1}{2} \times 8)=(4,4) \\ C'=\amp(\frac{1}{2}\times 12), (\frac{1}{2} \times 2)=(6,4) \\ D'=\amp(\frac{1}{2}\times 14), (\frac{1}{2} \times 8)=(7,1) \\ E'=\amp(\frac{1}{2}\times 10), (\frac{1}{2} \times 0)=(5,0) \\ \text{vertices of the image}= \amp A' (3,4), B'(4,4), C' (6,4), D' (7,1) \text{and} E' (5,O) \end{align*}

🔗

\begin{align*} A'=\amp(-1\times 6), (-1 \times 8)=(-6,-8) \\ B'=\amp(-1\times 8), (-1 \times 8)=(-8,-8) \\ C'=\amp(-1\times 12), (-1 \times 2)=(-12,-8) \\ D'=\amp(-1\times 14), (-1 \times 8)=(-14,-2) \\ E'=\amp(-1\times 10), (-1 \times 0)=(-10,0) \\ \text{vertices of the image}= \amp A' (-6,-8), B'(-8,-8), C' (-12,-8), D' (-14,-2) \text{and} E' (-10,0) \end{align*}

🔗

\(\textbf{Negative scale factor}\)

🔗

In the provided diagram, rectangle \(ABCD\) has been enlarged to form rectangle \(A'B'C'D'\text{,}\) with point \(O\) as the center of the enlargement.

🔗

Figure 2.1.15.

🔗

\(\textbf{Note:}\)

🔗

If an enlargement has a negative scale factor, the image is formed on the opposite side of the center and is inverted (Upside down).

🔗

The rectangle \(ABCD\) has been enlarged by a scale factor of \(-\frac{1}{2}\) .

🔗

Example 2.1.16.

🔗

Enlarge the triangle \(ABC\) by scale factor of \(-1\) about the point \(O\text{.}\)

🔗

Solution.

The centre of enlargement is \(O\text{,}\) the origin.

🔗

Draw a line from point \(A\) through \(O\) and extend the line upwards through the centre of enlargement.

🔗

Measure the distance from point \(O\) to point \(A\text{.}\) Since the scale factor is \(-1\text{,}\) and the distance from \(OA=5\text{,}\) then \(OA'=-1\times 5=-5\)

🔗

Similarly draw the lines from point \(B\) through \(O\) and \(C\) through \(O\) and extend the line upwards through the centre of enlargement. Measure the distance from point \(O\) to point \(B'\) and \(O\) to point \(C'\) and multipy by the scale factor \(-1\) to get the new distance from \(O\) to point \(B\) and \(O\) to point \(C\)

🔗

Join up the points to make the new triangle \(A'B'C'\)

🔗

🔗

Checkpoint 2.1.19. Enlargements (25-4).

Load the question by clicking the button below.

🔗

Checkpoint 2.1.20. Circumference of a Circle Under Enlargement.

Load the question by clicking the button below.

🔗

Checkpoint 2.1.21. Enlargement of a Triangle with Centre at the Origin.

Load the question by clicking the button below.

🔗

Checkpoint 2.1.22. Enlargement and Similarity Parsons Proof.

Load the question by clicking the button below.

🔗

Exercises Exercises

1.

A triangle with the verticies \(X\, (4,0)\text{,}\) \(Y\, (6,3)\) and \(Z\, (5,4)\) is enlarged.If the centre of enlargment is \((1,1)\text{,}\) find the co-ordinates of the image of the triangle when the scale factor is:

🔗

(a) \(-2\)

🔗

(b) \(\frac{1}{2}\)

🔗

2.

Points \(A\, (2,6)\text{,}\) \(B\, (4,6)\text{,}\) and \(C\, (4,2)\) are the vertices of a triangle. Taking point \((0,2)\) as the centre of enlargement, find the coordinates of its image when the scale factor is \(-1\text{.}\)

🔗

3.

Points \(P\,(1,4)\text{,}\) \(Q\, (3,4)\) and \(R\, (3,1)\) are verticies of a triangle. Taking the origin as the centre of enlargement, find the image when the scale factor is;

🔗

(a) \(-\frac{1}{4}\)

🔗

(b) \(-3\)

🔗

4.

A square measures \(5\, cm\) by \(9\,cm\text{.}\) Find the corresponding measurements of the image of the square after an enlargement with scale factor of \(-2.\)

🔗

5.

A photograph is enlarged so that its width increases from \(10\, cm\) to \(25\, cm\text{.}\) If the original height is \(15\, cm\text{,}\) find the new height.

🔗

6.

A map has a scale of \(1:50,000\text{.}\) If the distance between two cities on the map is \(8\, cm\text{,}\) find the actual distance.

🔗

Prev Top Next