Volume of Solids

Section 3.2 Volume of Solids

\(\textbf{Volume}\) is the amount of space occupied by a three-dimensional object. It tells us how much something can hold.

🔗

If an object is hollow, its volume tells us the capacity – how much liquid or air it can hold. If it is solid, volume tells us how much space it fills up.

🔗

For example,

🔗

Subsection 3.2.1 Volume of prisms

A \(\text{prism}\) is a solid with a uniform cross- section. The sides connecting the bases are parallelograms.

🔗

The volume \(\text{V}\) of a prism with cross section area \(\text{A}\) and length \(\text{l}\) is given by

\begin{equation*} \text{V} = \text{A} \times \text{l}\text{.} \end{equation*}

🔗

Subsubsection 3.2.1.1 Volume of triangular based prism

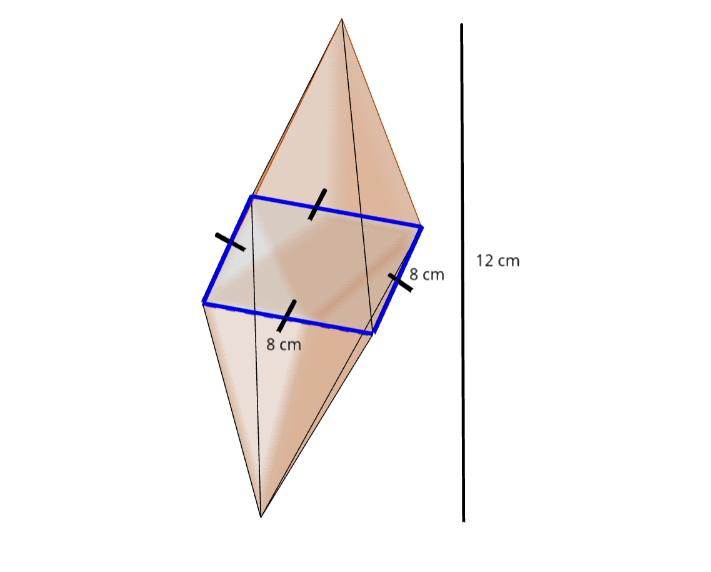
Activity 3.2.1.

\(\textbf{Work in pairs}\)

🔗

Instructions

🔗

Imagine you are designing a small water channel shaped like a triangular prism to carry water from a tank to a garden.
🔗

🔗
Below is a cross-sectional diagram of the triangular prism channel.
🔗
1. How many faces does the triangular prism above have?
  🔗
  
  🔗
🔗
🔗

🔗

Draw the triangular face and label its base and height.
🔗

🔗
Using the diagram, calculate:
🔗
1. The area of the triangular cross-section.
  🔗
  
  🔗
2. The volume of the prism (channel) that will hold water.
  🔗
  
  🔗
🔗
🔗
Discuss with your partner:
🔗
1. What is the relationship between the base area and the volume of the prism?
  🔗
  
  🔗
2. How does changing the height of the prism affect its volume?
  🔗
  
  🔗
🔗
🔗

🔗

Key Takeaway

🔗

The figure shown below represents a triangular prism with a cross section area of \(\text{A}\) and a length of \(\text{l}\text{.}\)

🔗

The volume of a triangular prism is found by multiplying the area of its triangular cross-section by its length. Which can be writen as,

🔗

\begin{equation*} \text{V} = \text{A} \times \text{l} \end{equation*}

🔗

Example 3.2.1.

Find the volume of a triangular prism with a base area of \(12 \, \text{cm}^2\) and a length of \(5 \, \text{cm}\text{.}\)

🔗

Solution.

To find the volume, we use the formula:

🔗

\begin{align*} \text{V} = \amp \text{A} \times \text{l}\\ =\amp 12 \, \text{cm}^2 \times 5 \, \text{cm} \\ =\amp 60 \, \text{cm}^3 \end{align*}

🔗

Therefore, the volume of the prism is \({\color{black} 60 \, \text{cm}^3}\text{.}\)

🔗

Example 3.2.2.

Find the area of the figure below.

🔗

Solution.

To find the area of the triangular prism, we need to calculate the area of the triangular base and the area of the three rectangular faces.

🔗

The base area of the triangle can be calculated using the formula:

🔗

\begin{align*} \text{Base area(A)} = \amp \frac{1}{2} \times \text{b} \times \text{h} \\ = \amp \frac{1}{2} \times 8 \, \text{m} \times 12 \, \text{m} \\ =\amp 48 \, \text{m}^2 \end{align*}

🔗

The volume of the above figure is given by;

🔗

\begin{align*} \text{Volume} =\amp \text{Base area} \times \text{length(l)}\\ =\amp 48 \, \text{m}^2 \times 20 \, \text{m} \\ =\amp 960 \, \text{m}^3 \end{align*}

🔗

Therefore, the volume of the triangular prism is \({\color{black} 960 \, \text{m}^3}\text{.}\)

🔗

Example 3.2.3.

A loading company makes loaders of triangular prism as shown below. If the loader holds \(30 \text{m}^3\) of soil, determine the length of the loader.

🔗

Solution.

\(\text{Volume} = \text{Cross-sectional area} \times \text{length(l)}\)

🔗

\(\text{Cross-sectionalarea}=\text{Area of triangle}\)

🔗

\begin{align*} \text{Height}= \amp \sqrt{(\sqrt{8})^2-2^2} \\ = \amp \sqrt{8-4} \\ =\amp \sqrt{4} \\ =\amp 2 \,\text{m} \end{align*}

🔗

\begin{align*} \text{Area of triangle}= \amp \frac{1}{2} \times \text{Base} \times \text{Height} \\ =\amp \frac{1}{2} \times 2 \times 2 \\ \amp = 2 \,\text{m}^2 \end{align*}

🔗

Volume is given by:

🔗

\begin{align*} \text{Volume} = \amp \text{Cross-sectional area} \times \text{length(l)} \\ 30 =\amp 2 \times l \\ l = \amp \frac{30}{2} \,\text{m} \\ = \amp 15 \,\text{m} \end{align*}

🔗

Therefore, the length of the loader is \({\color{black} 15 \, \text{m}}\text{.}\)

🔗

Exercises Exercises

1.

🔗

2.

🔗

Subsubsection 3.2.1.2 Volume of rectangular based prism

Activity 3.2.2.

\(\textbf{Work in Pairs}\)

🔗

\(\textbf{Instructions}\)

🔗

Observe the school’s water tank or storage box.
🔗

🔗
Using a rectangular water tank as an example:
🔗

Measure (or estimate) its:
🔗
1. Length
  🔗
  
  🔗
2. Width
  🔗
  
  🔗
3. Height
  🔗
  
  🔗
🔗
🔗
Calculate the volume of the rectangular water tank.
🔗

🔗
Convert the volume to litres.
🔗

🔗
Discuss in your group:
🔗

How do we find the volume of a rectangular prism?
🔗

🔗

🔗

Play along with the sliders below to explore the volume of a rectangular prism.

🔗

Figure 3.2.4. Volume of a rectangular prism

🔗

\(\textbf{Key Takeaway}\)

🔗

Given a rectangular prisim like the one shown below,

🔗

The volume of a rectangular prism is given by the formula:

🔗

\(\text{Volume}= \text{Base area} \times \text{Height}\)

🔗

Which can be written as:

\begin{equation*} V= l \times w \times h \end{equation*}

🔗

Example 3.2.5.

Work out the volume of the rectangular prism shown below.

🔗

Solution.

\(\text{Volume}= \text{Base area} \times \text{Height}\)

🔗

\begin{align*} \text{Base area} =\amp \text{length(l)} \times \text{width(w)}\\ = \amp 12 \times 9 \\ =\amp 108 \text{ cm}^2 \end{align*}

🔗

\begin{equation*} \text{Height}= 20 \, \text{cm} \end{equation*}

🔗

\begin{align*} \text{Volume}= \amp 108 \text{ cm}^2 \times 20 \, \text{cm}\\ =\amp 2160 \text{ cm}^3 \end{align*}

🔗

Therefore, the volume of the rectangular prism is \({\color{black} 2160 \, \text{cm}^3}\text{.}\)

🔗

Example 3.2.6.

The Volume of a rectangular based prism is \(720 \, \text{cm}^3\text{.}\) The height of the prism is \(10 \, \text{cm}\text{.}\) What is the base area of the prism?

🔗

Solution.

We know that the volume of a prism is given by the formula:

🔗

\(\text{Volume}= \text{Base area} \times \text{Height}\)

🔗

Rearranging the formula to find the base area gives:

🔗

\(\text{Base area} = \frac{{\text{Volume}}}{\text{Height}}\)

🔗

Substituting in the known values:

🔗

\begin{align*} \text{Base area} = \amp \frac{720 \, \text{cm}^3}{10 \, \text{cm}}\\ \amp 72 \, \text{cm}^2 \end{align*}

🔗

Therefore, the base area of the prism is \({\color{black} 72 \, \text{cm}^2}\text{.}\)

🔗

Example 3.2.7.

A movie theater serves ice creams in two different containers.

🔗

Calculate the volume of each container.
🔗

🔗
Which container holds more ice cream?
🔗

🔗

🔗

Solution.

The volume of container (i) is given by:
🔗

\begin{align*} \text{Volume} = \amp l \times w \times h\\ =\amp 4 \, \text{m} \times 7 \, \text{m} \times 10 \, \text{m}\\ =\amp 280 \, \text{m}^3 \end{align*}

🔗

The volume of container (ii) is given by:
🔗

\begin{align*} \text{Volume} = \amp \text{Base Area} \times \text{Height}\\ =\amp 9 \, \text{m} \times 8 \, \text{m} \times 8 \, \text{m}\\ =\amp 576 \, \text{m}^3 \end{align*}

🔗

Therefore,
🔗

The volume of container (i) is \({\color{black} 280 \, \text{m}^3}\)
🔗

The volume of container (ii) is \({\color{black} 576 \, \text{m}^3}\text{.}\)
🔗

🔗
Which container holds more ice cream?
🔗

Container (ii) holds more ice cream since \({\color{black} 576 \, \text{m}^3}\) is greater than \({\color{black} 280 \, \text{m}^3}\text{.}\)
🔗

🔗

🔗

Exercises Exercises

1.

🔗

2.

🔗

Subsection 3.2.2 Volume of pyramids

Activity 3.2.3.

Work in Groups

🔗

What you need

🔗

A ruler, a pencil, and a piece of paper.
🔗

🔗
A model of a net pyramid (you can make one using paper or cardboard).
🔗

🔗

🔗

Instrucrions

🔗

Using the ruler, construct the net square base pyramid on the paper like the one shown below.
🔗

Figure 3.2.10. A square base of a pyramid
🔗
🔗
Construct three such nets and fold them to form three pyramids.
🔗

🔗
Assemble them to make a cube.
🔗

🔗
What is the volume of the cube you have made from the pyramids?
🔗

🔗
What is the volume of one pyramid?
🔗

What do you notice about the relationship between the volume of the cube and the volume of one pyramid?
🔗

🔗
Discuss your findings with other groups.
🔗

🔗

🔗

\(\textbf{Activity 2}\)

🔗

Use this worksheet below to practice finding the Volume of a Triangular Pyramid.
🔗

🔗
Adjust the height, base, and base_1 using the labeled sliders.
🔗

🔗
Answer the questions below. \(\textbf{Use the multi-colored switches to check your work.}\)
🔗

🔗

🔗

Figure 3.2.11. Volume of a triangular pyramid

🔗

Definition 3.2.12.

A \(\textbf{pyramid}\) is a solid shape that has a flat base and triangular sides that meet at a point at the top, called the apex.

🔗

Key Takeaway

🔗

The volume of a pyramid is one-third the area of its base multiplied by its height. This means that if you know the area of the base and the height, you can easily find the volume.

🔗

Therefore, the volume of each pyramid is given by:

🔗

\(\textbf{Volume}= \frac{1}{3}(\text{Base Area(A)} \times \text{Height(h)})\)

🔗

Which can be written as;

🔗

\begin{equation*} V= \frac{1}{3}(A\times h) \end{equation*}

🔗

Where, where \(A\) is the area of the base and \(h\) the perpendicular height of the pyramid

🔗

Example 3.2.13.

Find the volume of te figure below.

🔗

Solution.

To find the volume of the pyramid, we use the formula:

🔗

\begin{align*} \text{Volume} \amp \text{Base Area} \amp \text{Height} \end{align*}

🔗

The base area is a rectangle with length \(6 \, \text{cm}\) and width \(4 \, \text{cm}\text{,}\) so:

🔗

\begin{align*} \text{Base area } =\amp 6 \, \text{cm} \times 4 \, \text{cm} \\ =\amp 24 \, \text{cm}^2 \end{align*}

🔗

\begin{align*} \text{Volume} = \amp \frac{1}{3}(\text{Base Area} \times \text{Height})\\ =\amp \frac{1}{3}(24 \, \text{cm}^2 \times 8 \, \text{cm}) \\ =\amp \frac{1}{3}(192 \, \text{cm}^3) \\ =\amp 64 \, \text{cm}^3 \end{align*}

🔗

Therefore, the volume of the pyramid is \({\color{black}64 \, \text{cm}^3}\text{.}\)

🔗

Example 3.2.14.

Calculate the volume of the following pyramids:

🔗

Triangular based with equal sides each measuring \(10 \, \text{cm}\) and a height of \(30\, \text{cm}\text{.}\)
🔗

(Give your answer to \(2\) decimal places)
🔗

🔗
Square based of sides \(12 \, \text{cm}\) and a height of \(25\, \text{cm}\text{.}\)
🔗

🔗
Rectangular based of sides \(12 \, \text{cm}\) and \(16 \, \text{cm}\) and slant edge \(26\, \text{m}\text{.}\)
🔗

🔗

🔗

Solution.

Triangular based pyramid
🔗

Since the base is triangular, we first find the area of the base.
🔗

\begin{align*} \text{Base of the triangle}= \amp \sqrt{10^2 - 5^2}\\ =\amp \sqrt{100 - 25}\\ =\amp \sqrt{75}\\ =\amp 5\sqrt{3} \, \text{cm}\\ =\amp 8.66 \, \text{cm} \end{align*}

🔗

The area of the base triangle is given by:
🔗

\begin{align*} \text{Area} = \amp \frac{1}{2} \times \text{Base} \times \text{Height}\\ = \amp \frac{1}{2} \times 8.66 \times 10 \, \text{cm}^2\\ = \amp 43.30 \, \text{cm}^2 \end{align*}

🔗

The volume of the pyramid is given by:
🔗

\begin{align*} \text{Volume} = \amp \frac{1}{3} \times \text{Base Area} \times \text{Height}\\ = \amp \frac{1}{3} \times 43.30 \times 30 \, \text{cm}^3\\ = \amp 433.00 \, \text{cm}^3 \end{align*}

🔗

🔗
Square based pyramid
🔗

Since the base is square, we first find the area of the base.
🔗

\begin{align*} \text{Area} = \amp \text{Side}^2 = 12^2 = 144 \, \text{cm}^2 \end{align*}

🔗

The volume of the pyramid is given by:
🔗

\begin{align*} \text{Base Area} = \amp 12^2 = 144 \, \text{cm}^2\\ = \amp 144 \, \text{cm}^2 \end{align*}

🔗

\begin{align*} \text{Volume} = \amp \frac{1}{3} \times \text{Base Area} \times \text{Height}\\ = \amp \frac{1}{3} \times 144 \times 25 \, \text{cm}^3\\ = \amp 1200.00 \, \text{cm}^3 \end{align*}

🔗

🔗
Rectangular-based pyramid
🔗

Base sides: \(12 \, \text{m} \, \text{by} \, 16 \, \text{m}\)
🔗

Slant edge \(= 26 \, \text{m}\)
🔗

Find height using Pythagoras theorem that is find half of base diagonal:
🔗

\begin{align*} \text{d} =\amp \sqrt{(12^2 + 16^2)} \\ = \amp \sqrt{(144 + 256)} \\ = \amp \sqrt{400} \\ = \amp 20 \, \text{m} \end{align*}

🔗

Use slant edge (\(26 \, \text{m}\)) as hypotenuse to find height:
🔗

\begin{align*} \text{h} =\amp \sqrt{(26^2 - 10^2)} \\ = \amp \sqrt{(676 - 100)} \\ = \amp \sqrt{576} \\ = \amp 24 \, \text{m} \end{align*}

🔗

The base area is gotten by:
🔗

\begin{align*} \text{Base Area} = \amp \text{Length} \times \text{Width} \\ = \amp 12 \, \text{m} \times 16 \, \text{m} \\ = \amp 192 \, \text{m}^2 \end{align*}

🔗

The volume of the pyramid is given by:
🔗

\begin{align*} \text{Volume} = \amp \frac{1}{3} \times \text{Base Area} \times \text{Height}\\ = \amp \frac{1}{3} \times 192 \times 24 \, \text{m}^3\\ = \amp 1536.00 \, \text{m}^3 \end{align*}

🔗

🔗

🔗

Therefore, the volumes of the pyramids are:

🔗

Triangular based pyramid: \({\color{black}433.00 \, \text{cm}^3}\)
🔗

🔗
Square based pyramid: \({\color{black}1200.00 \, \text{cm}^3}\)
🔗

🔗
Rectangular based pyramid: \({\color{black}1536.00 \, \text{m}^3}\)
🔗

🔗

🔗

Example 3.2.15.

A crystal is in the form of two similar square based pyramids joined at their bases as shown below. Calculate the volume of the crystal if the height of the whole crystal.

🔗

Solution.

The volume of a pyramid is given by the formula:

🔗

\begin{align*} \text{Volume} = \amp \frac{1}{3} \times \text{Base Area} \times \text{Height} \end{align*}

🔗

The base area of a square pyramid is given by the formula:

🔗

\begin{align*} \text{Base Area} = \amp \text{Side}^2\\ =\amp 8^2 \\ =\amp 64 \, \text{cm}^2 \end{align*}

🔗

The volume of the crystal pyramid is given by:

🔗

\begin{align*} \text{Volume} = \amp \frac{1}{3} \times \text{Base Area} \times \text{Height}\\ = \amp \frac{1}{3} \times 64 \, \text{cm}^2 \times 12 \, \text{cm}\\ = \amp \frac{768}{3} \, \text{cm}^3\\ = \amp 256.00 \, \text{cm}^3 \end{align*}

🔗

Therefore, the volume of the crystal is \({\color{black}256 \, \text{cm}^3}\text{.}\)

🔗

Exercises Exercises

1.

🔗

2.

🔗

Subsection 3.2.3 Volume of a cone

Activity 3.2.4.

\(\textbf{Work in groups}\)

🔗

What you need

🔗

A plastic or paper cone (e.g. party hat or funnel)
🔗

🔗
A cylinder of the same base radius and height as the cone (e.g. a cut bottle or measuring cylinder)
🔗

🔗
Rice or sand
🔗

🔗
A measuring jug (optional)
🔗

🔗

🔗

Instructions

🔗

Observe the cone and the cylinder you have. Confirm that their base radii and heights are equal.
🔗

🔗
Fill the cone with rice or sand until it is full.
🔗

🔗
Pour the rice or sand from the cone into the cylinder.
🔗

🔗
Repeat filling the cone and pouring into the cylinder.
🔗

🔗
Count how many times you need to fill the cone to completely fill the cylinder.
🔗

🔗
How many cones of rice or sand are needed to fill the cylinder?
🔗

How do you find the volume of a cone?
🔗

🔗
Share your findings with other learners in the class.
🔗

🔗

🔗

\(\textbf{Activity 2}\)

🔗

Play along with the tabs,sliders to explore how the volume of a cone changes with its height and radius.

🔗

Figure 3.2.16. Volume of a cone

🔗

Definition 3.2.17.

A \(\textbf{cone}\) is a right pyramid with a circular base

🔗

In the limit, as the number of faces approaches infinity, the shape is a cone.

🔗

Play along with the interactive figure below to see how cone is formed from a pyramid.

🔗

Figure 3.2.18. A cone formed from a pyramid

🔗

\(\textbf{Key Takeaway}\)

🔗

From your activity, it takes three cones to fill a cylinder with the same base and height. This tells us that the cone’s volume is \(\textbf{one-third}\) the volume of the cylinder.

🔗

Therefore the volume is given by?

\begin{equation*} \textbf{Volume of a cone} = \frac{1}{3} \pi r^2 h \end{equation*}

🔗

Where \(r\) is the radius of the base and \(h\) is the height of the cone.

🔗

Example 3.2.19.

Calculate the volume of the cone shown below. (Take \(\pi=\frac{22}{7}\))

🔗

Solution.

\(\text{Volume of a cone} = \frac{1}{3} \times \text{Base Area} \times \text{Height}\)

\begin{equation*} = \frac{1}{3} \times \pi r^2 \times h \end{equation*}

🔗

\begin{align*} \text{Volume}= \amp \frac{1}{3} \times \pi r^2 \times h \\ =\amp \frac{1}{3} \times \frac{22}{7} \times 14^2 \times 28 \\ =\amp \frac{1}{3} \times \frac{22}{7} \times 196 \times 28 \\ =\amp \frac{1}{3} \times \frac{22}{7} \times 5488 \\ =\amp \frac{1}{3} \times 22 \times 784 \\ =\amp \frac{17248}{3} \\ =\amp 5749.33 \text{ cm}^3 \end{align*}

🔗

Therefore, the volume of the cone is \({\color{black}5749.33 \text{ cm}^3}\text{.}\)

🔗

Example 3.2.20.

A party hat has the shape of a cone. The volume of the hat is \(462 \, \text{cm}^3\text{.}\) The hat has a perpendicular height of \(17 \, \text{cm}\text{,}\) find the radius of the base of the hat.

🔗

Solution.

The hat has the following dimensions:

🔗

Volume of hat = \(462 \, \text{cm}^3\text{,}\) height = \(17 \, \text{cm}\)

🔗

\begin{align*} \text{Volume of the hat}= \amp \frac{1}{3} \pi r^2 h\\ 462 = \amp \frac{1}{3} \pi r^2 (17)\\ 462 = \amp \frac{22}{21} \times 17 \times r^2\\ 462 \times 21 = \amp 22 \times 17 \times r^2\\ 9702= \amp 374 \times r^2\\ r^2= \amp \frac{9702}{374} \\ r= \amp \sqrt{\frac{9702}{374}}\\ r= \amp \sqrt{25.95} \\ r= \amp 5.5 \, \text{cm} \end{align*}

🔗

Therefore, the radius of the base of the hat is \({\color{black}5.5 \, \text{cm}}\text{.}\)

🔗

Example 3.2.21.

The figure below shows a model made from two cones. Determine the volume of the model. (Take \(\pi=3.142\))

🔗

Solution.

The model consists of two cones with the same base radius and height.

🔗

The height of each cone is \(10 \, \text{cm}\) and the radius of the base is \(3.5 \, \text{cm}\text{.}\)

🔗

The volume of one cone is given by the formula:

🔗

\begin{align*} \text{Volume} =\amp \frac{1}{3} \pi r^2 h\\ =\amp \frac{1}{3} \times 3.142 \times (3.5)^2 \times 20\\ =\amp \frac{1}{3} \times 3.142 \times 12.25 \times 20\\ =\amp \frac{1}{3} \times 3.142 \times 245\\ = \amp \frac{769.83}{3}\\ = \amp 256.61 \, \text{cm}^3 \end{align*}

🔗

Therefore, the volume of one cone is \({\color{black}256.61 \, \text{cm}^3}\text{.}\)

🔗

Exercises Exercises

1.

🔗

2.

🔗

Subsection 3.2.4 Volume of a frustum

Activity 3.2.5.

\(\textbf{Work in groups}\)

🔗

What you need

🔗

A cone-shaped paper cup
🔗

🔗
Scissors
🔗

🔗
Ruler
🔗

🔗

🔗

Instructions

🔗

Take the cone-shaped paper cup and measure its height and radius like the one below.
🔗

Figure 3.2.22. Conical cup
🔗
Record the (radius of base) and (height of whole cone).
🔗

🔗
Cut off the top part horizontally to create a frustum as shown below.
🔗

Figure 3.2.23. Frustum cup
🔗
Measure:
🔗
1. The radius of the new top
  🔗
  
  🔗
2. The height of the frustum
  🔗
  
  🔗
🔗
🔗
Find the volume of the smaller cone that was cut off you can see it below.
🔗

Figure 3.2.24. Smaller cone
🔗
🔗
Find the volume of the whole cone.
🔗

🔗
Find the volume of the frustum by subtracting the volume of the smaller cone from the volume of the whole cone.
🔗

🔗
Discuss how the volume of a frustum is be calculated.
🔗

🔗
Share your findings with the class.
🔗

🔗

🔗

\(\textbf{Key Takeaway}\)

🔗

When a cone or a pyramid is cut horizontally, The top part will be a smaller cone or pyramid, and the remaining part is called a frustum.

🔗

\(\text{Volume of frustum}= \text{Volume of the big pyramid or cone}- \text{Volume of the small pyramid or cone}\)

🔗

Which can be written as:

🔗

\begin{equation*} V=\frac{1}{3}\pi R^2 H- \frac{1}{3}\pi r^2 h \end{equation*}

🔗

Example 3.2.25.

The figure below shows a frustum of a cone. Find its volume if the height of the cone is \(24\, \text{cm}\)

🔗

Solution.

The volume of the frustum can be calculated using the formula:

🔗

\begin{align*} \text{Volume of frustum} = \amp \text{Volume of the big cone} - \text{Volume of the small cone}\\ = \amp \frac{1}{3}\pi R^2 H- \frac{1}{3}\pi r^2 h \\ = \amp \frac{1}{3} \times \frac{22}{7} \times 21^2 \times 24 - \frac{1}{3} \times \frac{22}{7} \times 7^2 \times 12\\ =\amp 11\,088-616\\ = \amp 10472 \, \text{cm}^3 \end{align*}

🔗

Therefore, the volume of the frustum is \({\color{black}10472\, \text{cm}^3}\)

🔗

Example 3.2.26.

A lampshade in the form of a frustum is cut from a cone of height \(40 \, \text{cm}\text{.}\) The bottom diameter of the lampshade is \(28 \, \text{cm}\) and the top diameter is \(14 \, \text{cm}\text{.}\) Calculate the volume of the lampshade if its vertical height is \(15 \, \text{cm}\text{.}\) (Take \(\pi= 3.142\)).

🔗

Solution.

The lampshade is in the form of frustum of a cone.

🔗

The diamension of the lampshade is given as:
🔗

\(\text{Radius of the bottom base} = \frac{28}{2} = 14 \, \text{cm}\)
🔗

\(\text{Radius of the top base} = \frac{14}{2} = 7 \, \text{cm}\)
🔗

\(\text{Height of the frustum} = 15 \, \text{cm}\)
🔗

\(\text{Height of the whole cone} = 40 \, \text{cm}\)
🔗

\(\text{Height of the small cone} = 40 - 15 = 25 \, \text{cm}\)
🔗

🔗

🔗

The volume of the frustum can be calculated using the formula:

🔗

\begin{align*} V= \amp \frac{1}{3}\pi R^2 H- \frac{1}{3}\pi r^2 h \\ = \amp \frac{1}{3} \times 3.142 \times 14^2 \times 40 - \frac{1}{3} \times 3.142 \times 7^2 \times 25\\ = \amp \frac{1}{3} \times 3.142 \times (14^2 \times 40 - 7^2 \times 25)\\ = \amp \frac{1}{3} \times 3.142 \times (7840 - 1225)\\ = \amp \frac{1}{3} \times 3.142 \times 6615\\ = \amp 6928.11 \, \text{cm}^3 \end{align*}

🔗

Therefore, the volume of the lampshade is \({\color{black}6928.11\, \text{cm}^3}\)

🔗

Example 3.2.27.

The diagram below is a pyramid. The upper part of the pyramid is cut off. Calculate the volume of the frustum formed.

🔗

Solution.

\(\text{Volume of frustum}= \text{Volume of the big pyramid}-\text{Volume of the small pyramid}\)

🔗

Volume of the big pyramid:

🔗

\begin{align*} \text{Volume of big pyramid}=\amp \frac{1}{3} \times \text{Base Area} \times \text{Height} \\ = \amp \frac{1}{3} \times 10 \times 8 \times 8 \\ = \amp \frac{1}{3 } \times 640\\ = \amp 213.33 \, \text{cm}^3 \end{align*}

🔗

Volume of the small pyramid:

🔗

\begin{align*} \text{Volume of small pyramid}= \amp \frac{1}{3} \times \text{Base Area} \times \text{Height} \\ = \amp \frac{1}{3} \times 5 \times 4 \times 4 \\ = \amp \frac{1}{3 } \times 80\\ = \amp 26.67 \, \text{cm}^3 \end{align*}

🔗

\begin{align*} \text{Volume of frustum}= \amp 213.33 \, \text{cm}^3- 26.67 \, \text{cm}^3 \\ = \amp 186.66 \, \text{cm}^3 \end{align*}

🔗

Therefore, the volume of the frustum formed is \({\color{black}186.66\, \text{cm}^3}\)

🔗

Exercises Exercises

1.

🔗

2.

🔗

Subsection 3.2.5 Volume of a sphere

Activity 3.2.6.

Work in Groups

🔗

\(\textbf{Play and Learn Activity: Discovering the Volume of a Sphere}\)

🔗

What you need:

🔗

A small ball (e.g. tennis ball, ping pong ball or football ball)
🔗

🔗
A measuring jug or graduated cylinder
🔗

🔗
Water
🔗

🔗
A string or tape measure
🔗

🔗

🔗

Instructions

🔗

Predict: How much space (volume) the ball will take up.
🔗

🔗
Measure the radius:
🔗

Use the string or tape measure to find the diameter of the ball.
🔗

Divide by \(2\) to get the radius (r).
🔗

🔗
Find the volume practically:
🔗
1. Fill the measuring jug halfway with water. Note this initial volume (V₁).
  🔗
  
  🔗
2. Submerge the ball completely in the water. Note the new volume (V₂).
  🔗
  
  🔗
3. Calculate the volume of the ball as:
  🔗
  
  \(V = V_2 - V_1\)
  🔗
  
  🔗
🔗
🔗
Record your results.
🔗

🔗
Compare your predicted volume with the actual volume you measured.
🔗

🔗
Discuss with other learners how to calculate the volume of a sphere.
🔗

🔗

🔗

In the interactive simulation below, play along with the radius to identify the volume of a sphere.

🔗

Figure 3.2.28. Volume of a sphere

🔗

\(\textbf{Key Takeaway}\)

🔗

The volume of a sphere is given by:

🔗

\begin{equation*} \textbf{Volume}= \frac{4}{3} \pi r^3 \end{equation*}

🔗

Where \(r\) is the radius of the sphere.

🔗

Example 3.2.29.

Find the volume of the figure below: (Use \(\pi = \frac{22}{7}\))

🔗

Solution.

The radius of the sphere is given as \(28 \text{ cm}\text{.}\)

🔗

The volume is given by:

🔗

\begin{align*} \text{Volume} =\amp \frac{4}{3} \pi r^3\\ = \amp \frac{4}{3} \times \frac{22}{7} \times (28)^3\\ = \amp \frac{4 \times 22 \times 28^3}{3 \times 7} \text{ cm}^3\\ = \amp 10922.67 \text{ cm}^3 \end{align*}

🔗

The volume of the sphere is \({\color{black}10922.67 \text{ cm}^3}\text{.}\)

🔗

Example 3.2.30.

Moraa made a spherical cake balls of diameter \(4.2 \text{ cm}\text{.}\) If she had a minced cake of \(194.05\, \text{cm}^3\text{,}\) find the number of cake balls she made from the minced cake.

🔗

Solution.

Find the radius of one cake ball:

🔗

The radius is half of the diameter:

🔗

\begin{equation*} r = \frac{4.2}{2} = 2.1 \text{ cm} \end{equation*}

🔗

Find the volume of one cake ball

🔗

\begin{align*} \text{Volume }= \amp \frac{4}{3} \pi r^3\\ = \amp \frac{4}{3} \times \frac{22}{7} \times (2.1)^3\\ = \amp \frac{4 \times 22 \times 2.1^3}{3 \times 7} \text{ cm}^3\\ = \amp 38.808 \,\text{ cm}^3 \end{align*}

🔗

Find the number of cake balls

🔗

\begin{align*} \textbf{Number of balls}= \amp \frac{\text{Total volume}}{\text{Volume of one ball}} \\ = \amp \frac{194.05}{38.808} \\ = \amp 5 \, \text{ balls} \end{align*}

🔗

Therefore, Moraa made \({\color{black}5 \, \text{ balls}}\) cake balls from the minced cake.

🔗

Example 3.2.31.

The figure below shows a globe with a radius of \(35 \text{ m}\text{.}\) Find its volume.(Use \(\pi=3.142\))

🔗

Solution.

The radius of the globe is given as \(28 \text{ m}\text{.}\)

🔗

The volume is given by:

🔗

\begin{align*} \text{Volume} =\amp \frac{4}{3} \pi r^3\\ = \amp \frac{4}{3} \times 3.142 \times (28)^3\\ = \amp \frac{4 \times 3.142 \times 28^3}{3} \text{ m}^3\\ = \amp 91964.24533 \text{ m}^3 \end{align*}

🔗

The volume of the globe is \({\color{black} 91964.25 \text{ m}^3}\text{.}\)

🔗

Exercises Exercises

1.

🔗

Technology 3.2.32.

\(\textbf{Technology Integration: Exploring Volume of Solids}\)

🔗

To learn more about volume of solids, explore these interactive and insightful resources:

🔗

\(\textbf{CK-12 Interactive Geometry}\) Engage with interactive explanations and practice problems to deepen your understanding of the volume of various solids including prisms, cylinders, spheres, and cones. Visit CK-12 Interactive Geometry
🔗

🔗
\(\textbf{YouTube Video – Visual Explanation}\) Gain a clear and concise understanding of calculating the volume of solids with this engaging video tutorial, perfect for visual learners. Watch Now
🔗

🔗

🔗

Prev Top Next