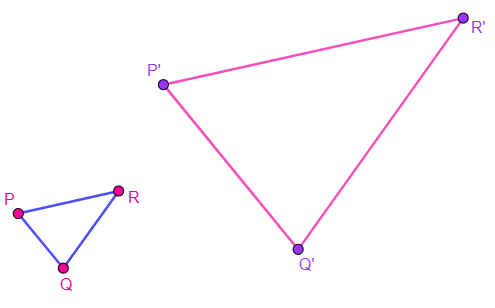
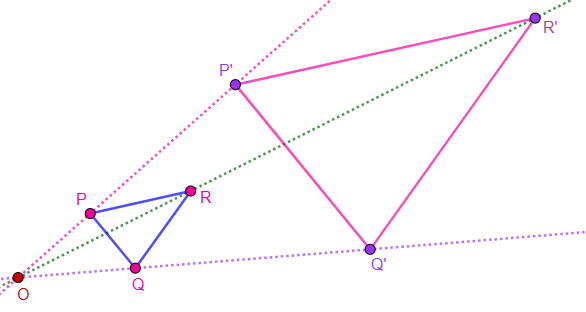
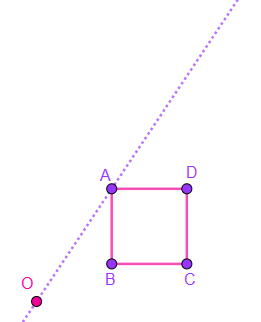
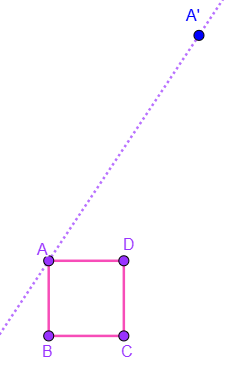
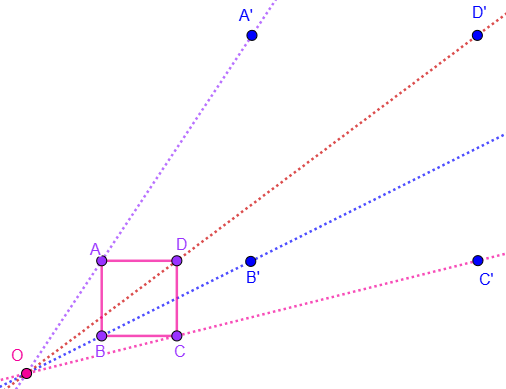
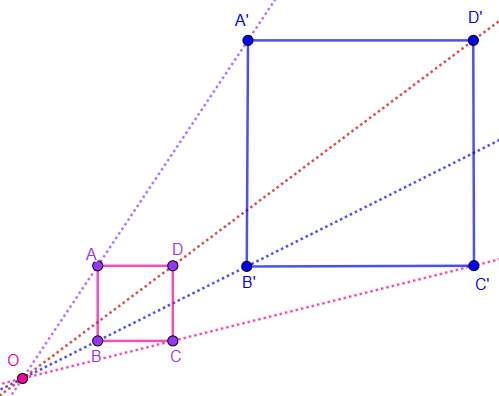
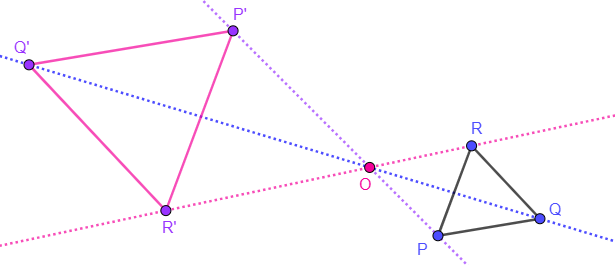
Activity 4.3.1.
\(\textbf{Work in groups}\)
-
Gather various objects found around the school.
-
Organize the items by grouping those with similar shapes.
-
Explain the reasons why you think the shapes are alike.
-
Present your findings and explanations to the other groups in the class.