Definition 3.1.1.
\(\textbf{Polygon}\)
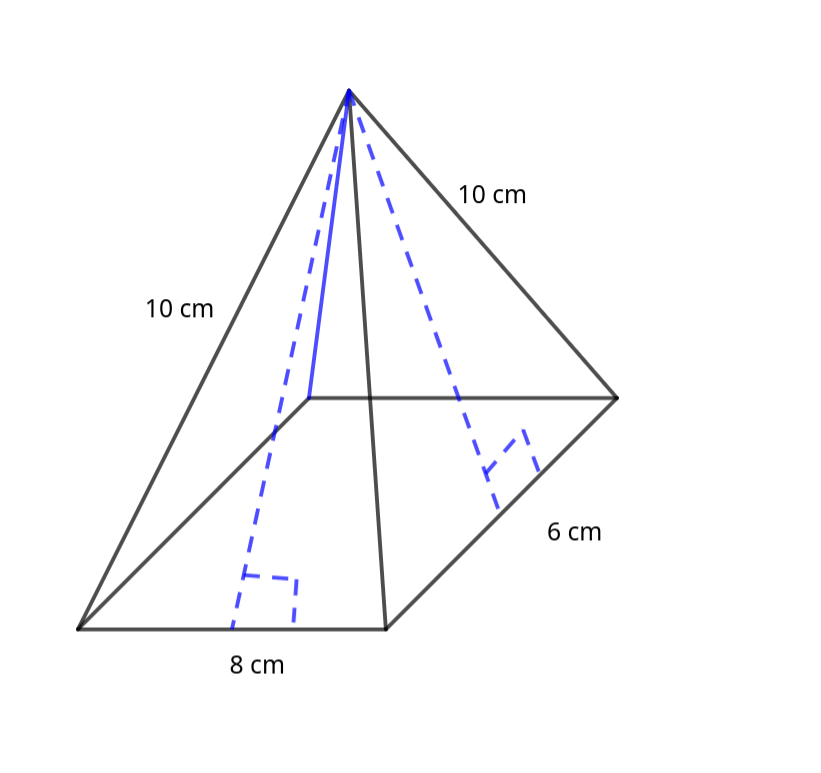
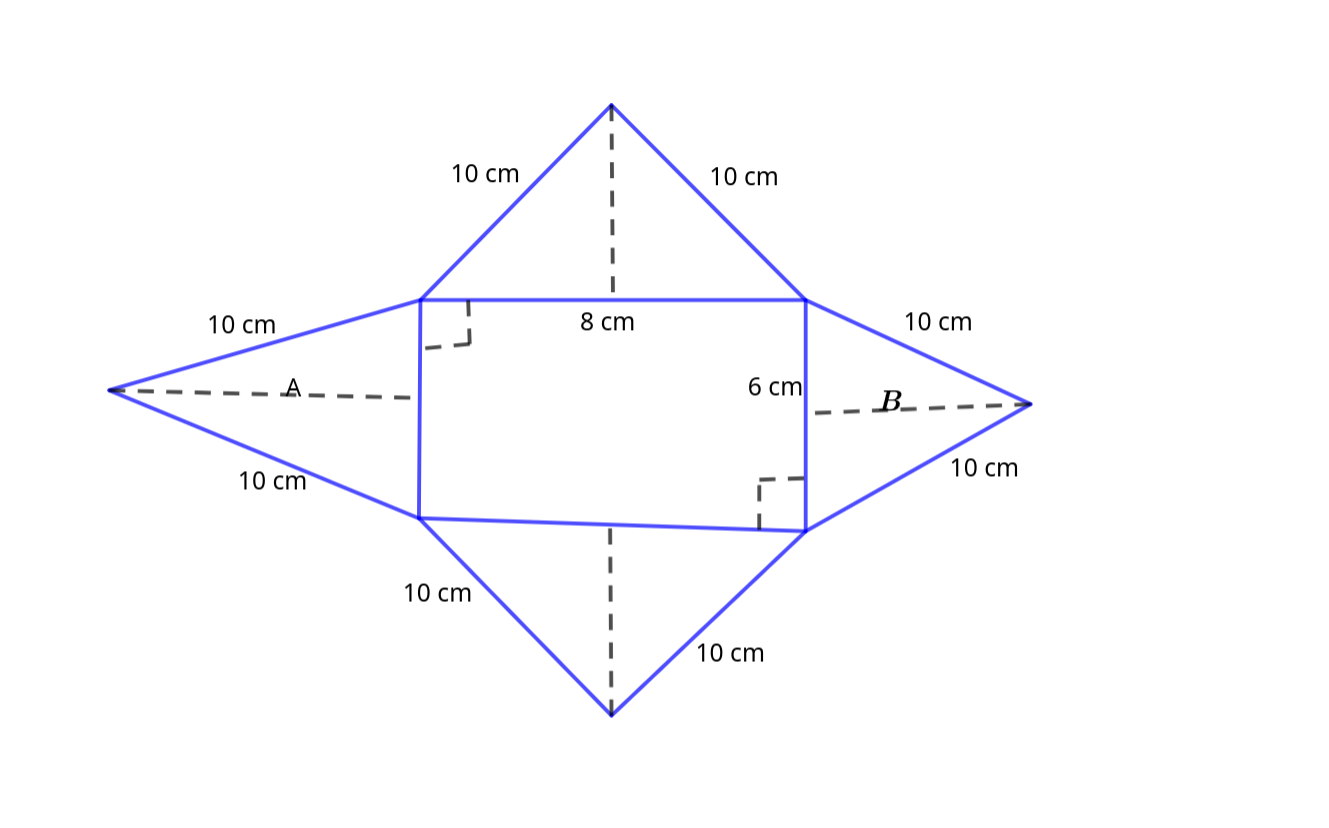
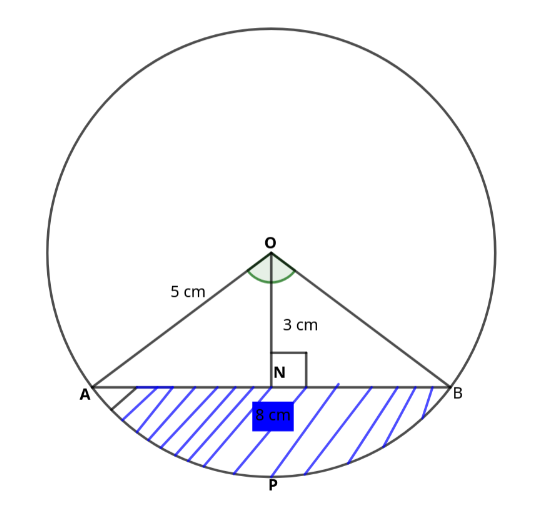
A polygon is a closed 2D shape made up of straight lines. Examples include \(\textbf{triangles, quadrilaterals, pentagons}\) and \(\textbf{hexagons.}\)
Section 3.1 Area
In our day-to-day life, we often encounter shapes and objects whether it’s the surface of a table, the wall of a house, the face of a pyramid, or even a football pitch.
Understanding area helps us measure how much space these flat surfaces cover.
Subsection 3.1.1 Area of regular and irregular polygons
Key Takeaway
A polygon can be either regular or irregular.
Below are some characteristics of polygons:
Type of Polygon
|
Characteristics
|
Examples
|
|---|---|---|
Regular Polygon
|
All sides are equal in length
All interior angles are equal
It is symmetrical
|
Equilateral triangle, square, regular hexagon
|
Irregular Polygon
|
Sides are not all equal
Angles are not all equal
Not symmetrical
|
Scalene triangle, rectangle, trapezium
|
Subsubsection 3.1.1.1 Area of a Pentagon
Activity 3.1.1.
Work in Groups
What you need.
Instructions
-
Use a ruler and a protractor to draw a regular pentagon as the one shown below.
-
Carefully cut out the pentagon using scissors.
-
Find the center of the pentagon.Divide the pentagon into \(5\) equal isosceles triangles by drawing straight lines from the center of the pentagon to each vertex (corner) as the one shown below:
-
Measure the side length and apothem \(\text{H}\) (a line from the center perpendicular to a side).
-
Label all sides and angles of the triangles.
-
Calculate the Area of the pentagon
-
Discuss if different-sized pentagons give different areas and why.
-
Discuss your findings with other groups.
Definition 3.1.2.
\(\textbf{pentagon }\)" comes from the Greek words "penta," meaning five, and "gon," meaning angle.
Therefore,
A \(\textbf{pentagon }\) is a flat, closed shape that has five straight sides and five angles.
Key Takeaway
-
A regular pentagon has equal sides and angles. It’s aea is given by:\begin{equation*} \text{Area} = \frac{1}{2} \times \text{Perimeter} \times \text{Apothem} \end{equation*}Where \(\text{Perimeter}= \text{Length} \times \text{Sides}\) and \(\text{Apothem }\)is the distance from the center of a regular polygon to aside.
Example 3.1.3.
Find the area of the figure below:
Solution.
To find the area of the given pentagon, we use the formula:
\begin{equation*}
\text{Area} = \frac{1}{2} \times \text{Perimeter} \times \text{apothem}
\end{equation*}
Since \(\text{Apothem} = 12.4 \, \text{ft}\, \text{and}\,\text{Side length} = 18\, \text{ ft} \)
\(\text{Perimeter}=5 \times 18\, \text{ ft}=90 \, \text{ft}\)
Therefore,
\begin{align*}
\text{Area}=\amp \frac{1}{2} \times 90 \times 12.4\\
=\amp 45 \times 12.4\\
=\amp 558 \, \text{ft}^2
\end{align*}
Example 3.1.4.
A gardener is designing a regular pentagonal flower bed. Each side of the flower bed is \(6\, \text{m}\text{,}\) and the distance from the center of the flower bed to the midpoint of a side is \(4.1 \, \text{m}\text{.}\) Find the area of the flower bed.
Example 3.1.5.
A regular pentagon has a side length of \(10 \, \text{cm}\) and an apothem of \(7.5 \, \text{cm}\text{.}\) Calculate its area.
Exercises Exercise
1.
2.
Subsubsection 3.1.1.2 Area of hexagon
Activity 3.1.2.
Work in Groups
What you need:
Instructions
-
LExplore the hexagon below:
-
How many sides does it have?
-
Measure the side \(\text{s}\) of the hexagon.
-
Are the sides equal in length?
-
-
\(\textbf{Divide the Hexagon into Triangles}\)The Hexagon below has been divided from the center to each corner:
-
Find the area of one triangle and use it to work out the area of the whole hexagon.
-
How do you find the area of the hexagon?
-
Share and compare your answers with your group.
Definition 3.1.6.
The word "\(\textbf{hexagon}\)" comes from the Greek words "hexa," which means six, and "gon," which means corner or angle.
A \(\textbf{hexagon}\) is a flat shape with six straight sides and six corners (angles).
Key Takeaway
Below is a figure of a regular hexagon.It has six equal sides and equal angles.
It’s area is given by:
\(\text{Area}=\frac{1}{2} \times \text{Perimeter (P)} \times \text{apothem}\)
Where \(\text{Perimeter} = \text{Length} \times \text{Number of sides}\text{.}\)
\(\textbf{Or}\)
If the apothem and the side is known, use:
\begin{equation*}
\text{Area} = \frac{3\sqrt{3}}{2} \times \text{s}^2
\end{equation*}
Where \(\text{s}\) is the length of one side of the hexagon.
Example 3.1.7.
Find the area of the hexagon below.
Solution.
Example 3.1.8.
Bees build honeycombs using hexagonal cells. If each cell has a side length of \(7.5 \, \text{mm}\text{,}\) what is the area of one cell?
Solution.
The side length of the hexagonal cell is \(7.5 \, \text{mm}\text{.}\)
Therefore:
\begin{align*}
\text{Area} =\amp \frac{3\sqrt{3}}{2} \times \text{s}^2\\
=\amp \frac{3\sqrt{3}}{2} \times (7.5)^2\\
=\amp \frac{3\sqrt{3}}{2} \times 56.25\\
=\amp 146.1417869 \\
= \amp 146.142\, \text{km}^2
\end{align*}
This implies that, the area of one hexagonal cell is approximately \({\color{black}146.41 \, \text{km}^2}\text{.}\)
Example 3.1.9.
The figure below shows a regular hexagon with center x.
Find;
Solution.
-
The perimeter of the hexagon is:\begin{align*} \text{Perimeter} =\amp \text{Length} \times 6\\ =\amp 16 \times 6\\ =\amp 96 \, \text{m} \end{align*}
-
The area of the hexagon is:\begin{align*} \text{Area} =\amp \frac{1}{2} \times \text{Perimeter} \times \text{apothem}\\ =\amp \frac{1}{2} \times 96 \times 30\\ =\amp 48 \times 30\\ =\amp 1440 \, \text{m}^2 \end{align*}This implies that, the area of the hexagon is \({\color{black}1440 \, \text{m}^2}\text{.}\)
Example 3.1.10.
A regular hexagon has an area of \(54 \, \text{cm}^2\) . What is its side length?
Solution.
To find the side length of a regular hexagon given its area, we can use the formula:
\begin{align*}
\text{Area} =\amp \frac{3\sqrt{3}}{2} \times \text{s}^2
\end{align*}
Given that the area is \(54\, \text{cm}^2\text{,}\) we set up the equation:
\begin{align*}
54 =\amp \frac{3\sqrt{3}}{2} \times \text{s}^2
\end{align*}
To solve for \(\text{s}\text{,}\) we can rearrange the equation:
\begin{align*}
\text{s}^2 =\amp \frac{54 \times 2}{3\sqrt{3}}\\
=\amp \frac{108}{5.196152423}\\
=\amp 20.78460969\\
\text{s} =\amp \sqrt{20.78460969}\\
=\amp 4.559014114 \\
= \amp 4.559 \,\text{cm}
\end{align*}
Therefore, the side length of the regular hexagon is \({\color{black}4.559\, \text{cm}}\text{.}\)
Exercises Exercise
1.
2.
Subsection 3.1.2 Surface area of prism
Definition 3.1.11.
A prism is a solid with uniform cross-section.
The surface area of a prism is the total area of all its faces that means the areas of the two identical bases and all the side faces (called lateral faces).
Subsubsection 3.1.2.1 Surface area of triangular based prism
Activity 3.1.3.
Work in Groups
What you need.
-
Ruler
-
Tape
-
Scissors
-
A piece of paper and a pencil
-
Cardboard (to create your prism model)
Instructions
-
Draw the net of a triangular prism on the cardboard, just like the one shown below.
-
Cut out the net carefully along the edges.
-
Fold the net along the edges to form a triangular prism.
-
Secure the edges with tape or glue to hold the prism together as shown below.
-
Count the number of triangular and rectangular faces.
-
-
Measure:
-
The base and height of one of the triangular faces.
-
The length and width of the rectangular faces.
-
-
Calculate the area of:
-
Calculate the total surface area of the prism.
-
How did you find the surface area of the prism?
-
\(\displaystyle \text{Discuss your findings with your classmates.}\)
Key Takeaway>
-
A triangular prism has:
-
The surface area of a triangular prism is the sum of the areas of its \(2\) triangular bases and \(3\) rectangular faces.Hence,\begin{equation*} {\color{black}\text{Total SA}= 2(\text{(Area of triangle)})+ 3(\text{Area of rectangle})} \end{equation*}
Example 3.1.12.
The length of a trianglar prism is \(8 \, \text{cm}\text{.}\) The crosssectional of the prism is an isosceles triangle of sides \(5 \, \text{cm}\,,\,5 \, \text{cm}\,,\, 6\,\text{cm} \) and height \(4 \, \text{cm}\text{.}\) Calculate the total surface area of the prism.
Solution.
\begin{align*}
\text{Area of triangle}=\amp \frac{1}{2} \times \text{base} \times \text{height} \\
=\amp \frac{1}{2} \times 6 \, \text{cm} \times 4 \, \text{cm}\\
=\amp = 24 \, \text{cm}^2
\end{align*}
Area of the rectangular faces is given by:
\begin{align*}
\text{Area} =\amp \text{Base} \times \text{Height} \\
=\amp (8 \times 6) + (5 \times 8 )+(5 \times 8) \\
=\amp 48 +40+40\\
=\amp 128 \,\text{cm}^2\\
\text{Total surface Area }= \amp (2 \times 24) + 128\\
= \amp 48 + 128 \\
= \amp 176 \, \text{cm}^2
\end{align*}
Therefore,
\begin{equation*}
{\color{black}\text{Total Surface Area} = 148 \, \text{cm}^2}
\end{equation*}
Example 3.1.13.
Find the surface area of the triangular prism shown below:
Solution.
To find the surface area of the prism, we need to calculate the areas of the triangular base and the rectangular faces.
Area of the triangular base:
\begin{align*}
\text{Area}= \amp \frac{1}{2} \times 10 \, \text{m} \times 8 \, \text{m} \\
= \amp 40 \, \text{m}^2
\end{align*}
Area of the rectangular faces:
\begin{align*}
\text{Area}= \amp 30 \, \text{m} \times 8 \, \text{m} \\
= \amp 240 \, \text{m}^2
\end{align*}
Therefore, the total surface area of the prism is:
\begin{align*}
\text{Surface Area} = \amp (2 \times 40) + 240\\
= \amp 80 + 240 = 320 \, \text{m}^2
\end{align*}
\({\color{black}\text{Total Surface Area} = 320 \, \text{m}^2}\)
Example 3.1.14.
The figure below shows a triangular prism. Use the diagram to help you draw its net.
Checkpoint 3.1.15.
Subsubsection 3.1.2.2 Surface area of rectangular based prism
Activity 3.1.4.
\(\textbf{Work in groups}\)
What you need.
-
Rulers
-
Scissors
-
Grid paper
-
A nets of rectangular prisms (or students can sketch their own)
Instructions
-
Draw a rectangular prism on the grid paper like the one shown below.
-
How many rectangular faces does the prism have?
-
How many faces does the prism have in total?
What does \(l\,, w\,, h\,\) represent in the figure? -
-
Measure each side and label the dimensions.
-
Compute the area of each face and sum them up to find the total surface area.
-
What is the formula for the surface area of a rectangular prism?
-
Now draw the net of the rectangular prism like the one shown below.
-
Now, calculate the area of each face in the net.Compare if its the same as the total surface area you calculated before.
-
Disscuss your findings with the class.
\(\textbf{Key Takeaway}\)
-
The surface area of a rectangular prism is the total area of all six faces.
-
The surface area of a rectangular prism is calculated using the formula:\begin{equation*} \text{SA} = 2lw + 2lh + 2wh \end{equation*}
Example 3.1.16.
Work out the surface area of the closed rectangular prism below:
Solution.
The sides of the rectangular prism are:
-
Length (l): \(6 \, \text{cm}\)
-
Width (w): \(3 \, \text{cm}\)
-
Height (h): \(4 \, \text{cm}\)
The surface area (SA) of the rectangular prism can be calculated using the formula:
\begin{align*}
\text{SA} = \amp 2lw + 2lh + 2wh\\
= \amp 2(6\times 3)+2(6\times 4)+2(3\times 4)\\
= \amp 36 + 48 + 24\\
= \amp 108 \, \text{cm}^2
\end{align*}
\({\color{black}\text{Total Surface Area} = 108 \, \text{cm}^2}\)
Example 3.1.17.
A sheet of metal is used to make \(5\) identical closed rectangular prisms. Each prism measurering \(26 \, \text{m}\) by \(16 \, \text{m}\) by \(18 \, \text{m}\text{.}\) Calculate the total area of the metal sheet that is needed to make all the prisms.
Solution.
The surface area (SA) of one rectangular prism can be calculated using the formula:
\begin{align*}
\text{SA} = \amp 2lw + 2lh + 2wh\\
= \amp 2(26\times 16)+2(26\times 18)+2(16\times 18)\\
= \amp 832 + 936 + 576\\
= \amp 2344 \, \text{m}^2
\end{align*}
The total surface area of all \(5\) prisms is:
\begin{align*}
\text{Total surface area} =\amp 5 \times 2344 \\
=\amp 11720 \, \text{m}^2
\end{align*}
\begin{equation*}
{\color{blue}\text{Total Surface Area of 5 prisms} = 11720 \, \text{m}^2}
\end{equation*}
Example 3.1.18.
The net below forms a rectangular prism. Calculate the total surface area.
Solution.
The dimensions of the rectangular prism are:
-
Length (l): \(10 \, \text{km}\)
-
Width (w): \(5 \, \text{km}\)
-
Height (h): \(6 \, \text{km}\)
Therefore,
\begin{align*}
\text{TSA} =\amp 2lw + 2lh + 2wh\\
= \amp 2(10\times 5)+2(10\times 6)+2(5\times 6)\\
= \amp 100 + 120 + 60\\
=\amp 280 \, \text{km}^2
\end{align*}
\({\color{black}\text{Total Surface Area} = 280 \, \text{km}^2}\)
Exercises Exercises
1.
2.
Subsection 3.1.3 Surface area of pyramids
Definition 3.1.19.
A \(\textbf{Pyramid}\) is a solid with a polygonal base and slanting sides that meet at a common apex.
The surface area of a \(\textbf{Pyramid}\) is the sum of the area of the slanting faces and the area of the base.
Subsubsection 3.1.3.1 Surface area of triangular, square and rectangular based-pyramids
Activity 3.1.5.
\(\text{Work in groups}\)
What you need
Instructions
-
The pyramids model are as shown below.
\(\bullet\) What is the name of the above pyramids? -
Measure the edges of the rectangular-based pyramid
-
Cut and open the rectangular-based pyramid along the edges to reveal its net as shown below.
-
Find the area of each faces of the above net.
-
Find the surface area of the rectangular-based pyramid using the net.
-
What is the surface area of the triangular-based pyramid?
-
What is the surface area of the square-based pyramid?
-
What is the surface area of the pentagonal-based pyramid?
-
Repeat the above steps for the triangular-based and square-based pyramids.
-
Discuss your findings with other group members.
Key Takeaway
-
\begin{equation*} \text{Surface Area of Pyramids}=\text{Base Area}+\text{area of thefour triangular faces.} \end{equation*}\(\textbf{Note:}\)Understanding the \(\textbf{net}\) helps visualize and calculate total area easily.
Example 3.1.20.
Calculate the surface area of the pyramid below.
Solution.
The net of the above model is as shown below.
The base area is \(8 \times 6 = 48 \text{cm}^2\text{.}\)
The height of the triangular face.
\begin{align*}
\text{h}= \amp \sqrt{10^2-3^2} \\
= \amp 9.5394 \, \text{cm}
\end{align*}
The height of triangular face.
\begin{align*}
\text{h}= \amp \sqrt{10^2-4^2} \\
= \amp 9.165 \, \text{cm}
\end{align*}
Area of the triangles are as shown:
\begin{align*}
\text{Area}=\frac{1}{2}\times \text{base}\times \text{height}\\
= \amp \frac{1}{2} \times 8 \times 9.165 \times 2\\
= \amp 74.52 \, \text{cm}^2
\end{align*}
\begin{align*}
\text{Area}=\frac{1}{2}\times \text{base}\times \text{height}\\
= \amp \frac{1}{2} \times 6 \times 9.5394 \times 2\\
= \amp 57.23 \, \text{cm}^2
\end{align*}
The total surface area is given by:
\begin{align*}
\text{Total Surface Area}=\text{Base Area}+\text{Area of Triangles}\\
= \amp 48 + 74.52 + 57.23\\
= \amp 179.75 \, \text{cm}^2
\end{align*}
Therefore, the total surface area of the pyramid is \({\color{black}179.75 \, \text{cm}^2}\text{.}\)
Example 3.1.21.
A tent is shaped like a square-based pyramid. The base is \(3 \, \text{m}\) by \(3 \, \text{m}\) and each triangular side has a height of \(2.5 \, \text{m}\text{.}\) Find the amount of canvas needed to make the tent.
Solution.
The base area is given by;
\begin{gather*}
\text{Base Area} = \text{length} \times \text{width}\\
= 3 \times 3\\
= 9 \, \text{m}^2
\end{gather*}
The area of the triangular faces is given by:
\begin{gather*}
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}\\
= \frac{1}{2} \times 3 \times 2.5 \times 4\\
= 15 \, \text{m}^2
\end{gather*}
Therefore, the total surface area of the tent is \({\color{black}24 \, \text{m}^2}\text{.}\)
Example 3.1.22.
Find the area of the figure below:
Solution.
The net of the figure is as shown below:
The height of the pyramid is given by:
\begin{align*}
\text{h}=\amp \sqrt{7^2-3.5^2}\\
= \amp \sqrt{49-12.25}\\
= \amp \sqrt{36.75}\\
= \amp 6.06 \, \text{cm}
\end{align*}
The area of the pyramid is given by:
\begin{align*}
\text{A}=\amp \frac{1}{2} \times 7 \times 6.06\\
= \amp 21.21 \, \text{cm}^2
\end{align*}
The total area is given by:
\begin{align*}
= \amp 21.21 + 21.21 \times 4\\
= \amp 21.21 + 84.84\\
= \amp 106.05 \, \text{cm}^2
\end{align*}
Therefore, the total surface area of the pyramid is \({\color{blue}106.05 \, \text{cm}^2 }\text{.}\)
Exercises Exercises
1.
2.
Subsection 3.1.4 Area of a part of a circle
A circle can be divided into different parts, like a \(\textbf{sector}\) (a "pizza slice") or a \(\text{segment}\) (a part cut off by a chord). Each part has its own formula for finding the area.
Subsubsection 3.1.4.1 Area of a sector
Activity 3.1.6.
\(\textbf{Work in groups}\)
What you need
-
A model of a circle (e.g., a paper circle, a round object, or a drawing).
-
A protractor or a tool to measure angles.
-
A ruler or measuring tape to measure the radius.
Instruction
-
The figure below shows a circle with a radius of \(20 \, \text{cm}\) and a central angle of \(120^\circ\) degrees.
-
Name the shaded area in the figure above.
-
Find the area of the shaded part of the circle.
-
Deduce the formula for the area of a sector of a circle.
-
Share your findings with the other groups.
Definition 3.1.23.
A sector is a region bounded by two radii and an arc consisting of a minor and major sector.
A \(\textbf{minor}\) sector is the smaller area between the two radii, while a \(\textbf{major}\) sector is the larger area.
Key Takeaway
The figure below illustrates the difference between a minor and major sector.
The area of a sector is the fraction of the area of a circle. A whole circle corresponds to an angle of \(360^\circ\text{,}\) so the area of a sector with a central angle \(\theta\) is given by:
\begin{equation*}
\text{Area of a sector} = \frac{\theta}{360^\circ} \times \pi r^2
\end{equation*}
Example 3.1.24.
Find the area of the figure below:
Solution.
To find the area of the sector, we use the formula:
\(\text{Area of a sector} = \frac{\theta}{360^\circ} \times \pi r^2\)
\begin{align*}
\text{Area}= \amp \frac{60^\circ}{360^\circ} \times \pi (10 \,\text{m} )^2 \\
\text{Area}= \amp \frac{60}{360} \times \pi (100) \\
=\amp 52.36 \, \text{m}^2
\end{align*}
The area of the sector is \({\color{black}52.36 \,\text{m}^2}\text{.}\)
Example 3.1.25.
A sprinkler rotates and waters grass in a sector of \(90^\circ\text{.}\) If the water reaches \(12 \, \text{m}\) from the center, find the area of grass watered.
Solution.
From the problem, we know:
- Central angle \(\theta = 90^\circ\)
- Radius \(r = 12 \, \text{m}\)
We can now find the area of the sector using the formula:
\(\text{Area of a sector} = \frac{\theta}{360^\circ} \times \pi r^2\)
\begin{align*}
\text{Area}= \amp \frac{90^\circ}{360^\circ} \times \pi (12 \,\text{m})^2 \\
= \amp \frac{90}{360} \times \pi (144) \\
= \amp 113.10 \, \text{m}^2
\end{align*}
The area of the sector is \({\color{black}113.10 \,\text{m}^2}\text{.}\)
Example 3.1.26.
The area of a sector of radius \(21\,\text{m}\) is \(154 \,\text{m}^2\text{.}\) Find the angle subtended by the sector. (Use \(\pi =\frac{22}{7}\) for calculations.)
Solution.
To find the angle subtended by the sector, we can rearrange the formula for the area of a sector:
\(\text{Area of a sector} = \frac{\theta}{360^\circ} \times \pi r^2\)
\begin{align*}
154= \amp \frac{\theta}{360^\circ} \times \frac{22}{7} (21)^2 \\
= \amp \frac{\theta}{360^\circ} \times \frac{22}{7} (441) \\
= \amp \frac{\theta}{360^\circ} \times (1385.44) \\
\frac{\theta}{360^\circ} = \amp\frac{154}{1385.44} \\\
\theta =\amp \frac{154 \times 360^\circ}{1385.44} \\\
= \amp 39.93^\circ \
\end{align*}
The angle subtended by the sector is \({\color{black}39.93^\circ}\text{.}\)
Exercises Exercises
1.
2.
Subsubsection 3.1.4.2 Area of a segment
Activity 3.1.7.
\(\textbf{Work in groups}\)
\(\textbf{Instructions}\)
-
Use the checkboxes to highlight different parts (sector, triangle, segment).
-
Adjust the radius and angle to see how the area of the segment changes.
-
Figure 3.1.27. Area of a segment -
Find the area of the segment formed by the sector and the triangle above.
-
Share your findings with the other groups.
Definition 3.1.28.
A \(\textbf{segment}\) is the area between a chord and the arc it subtends.
A chord is a line segment connecting two points on the circle.
An arc is a part of the circumference of a circle.
Key Takeaway
The figure below illustrates a minor and a major segment of a circle.
The area of a segment is calculated using the formula:
\(\text{Area of Segment} = \text{Area of Sector} - \text{Area of Triangle}\)
Example 3.1.29.
Find the area Of the shadded region in the figure below: Use \(\pi = 3.142\text{.}\)
Solution.
To find the area of the shaded region (the segment), we will use the formula:
\(\text{Area of Segment} = \text{Area of Sector} - \text{Area of Triangle}\)
Area of the sector:
\(\text{Area of Sector} = \frac{\theta}{360^\circ} \times \pi r^2\)
\begin{align*}
\text{Area}= \amp \frac{80}{360} \times \pi \times 21^2\\
=\amp\frac{80}{360} \times 3.142 \times 21^2\\
=\amp 49.5 \text{ cm}^2
\end{align*}
Area of the triangle:
You need to find the height of the triangle using the formula:
\(H^2=b^2+h^2\)
\begin{align*}
h= \amp\sqrt{H^2-b^2}\\
= \amp\sqrt{21^2-2^2}\\
=\amp \sqrt{441-4}\\
=\amp \sqrt{437}\\
=\amp 20.88 \text{ cm}
\end{align*}
\(\text{Area of Triangle} = \frac{1}{2} \times \text{base} \times \text{height}\)
\begin{align*}
= \amp\frac{1}{2} \times 4 \times 20.88\\
=\amp 42.66 \text{ cm}^2
\end{align*}
Area of the segment is given by:
\begin{align*}
\text{Area of Segment} = \amp \text{Area of Sector} - \text{Area of Triangle} \\
=\amp 49.5 - 42.66 \\
=\amp 6.84 \text{ cm}^2
\end{align*}
The area of the shaded region (segment) is \({\color{black}6.84 \,\text{cm}^2}\text{.}\)
Example 3.1.30.
The figure below is a circle with center O and radius \(5 \,\text{cm}\text{.}\) If ON \(=3 \, \text{cm}\text{,}\) AB \(=8 \, \text{cm}\) and \(\angle \,\text{AOB} = 106.3^\circ\text{.}\) Find the area of the shaded region.
Solution.
\(\text{Area of Segment} = \text{Area of SectornOAPB} - \text{Area of Triangle OAB}\)
Area of the sector \(OAPB\) is given by:
\begin{align*}
\text{Area of Sector} =\amp \frac{\theta}{360^\circ} \times \pi r^2 =\\
=\amp \frac{106.3}{360} \times \pi \times 5^2\\
=\amp \frac{106.3}{360} \times 3.142 \times 25\\
=\amp 23.19 \text{ cm}^2
\end{align*}
Area of triangle \(OAB\) is given by:
\begin{align*}
\text{Area of Triangle} =\amp \frac{1}{2} \times \text{base} \times \text{height} \\
=\amp \frac{1}{2} \times 8 \times 3\\
=\amp 12 \text{ cm}^2
\end{align*}
Area of the shaded region (segment) is given by:
\begin{align*}
\text{Area of Segment} = \amp \text{Area of Sector} - \text{Area of Triangle} \\
=\amp 23.19 - 12 \\
=\amp 11.19 \text{ cm}^2
\end{align*}
The area of the shaded region (segment) is \({\color{black}11.19 \,\text{cm}^2}\text{.}\)
Example 3.1.31.
A round water tank lid has a radius of \(28 \,\text{cm}\text{.}\) A technician cuts out a segment with a central angle of \(90^\circ\) to create an inspection opening. Find the area of the segment removed.
Solution.
To find the area of the segment, we will use the formula:
\begin{gather*}
\text{Area of Segment} = \text{Area of Sector} - \text{Area of Triangle}
\end{gather*}
Area of the sector is given by:
\begin{align*}
\text{Area of Sector} = \amp \frac{\theta}{360^\circ} \times \pi r^2 \\
=\amp \frac{90}{360} \times \pi (28)^2 \\
=\amp \frac{1}{4} \times 3.142 \times 784 \\
=\amp 615.75 \, \text{cm}^2
\end{align*}
Area of the triangle formed by the radii and the chord is given by:
\begin{align*}
\text{Area of Triangle} = \amp \frac{1}{2} \times \text{base} \times \text{height} \\
=\amp \frac{1}{2} \times 28 \times 28 \times \sin(90^\circ) \\
=\amp \frac{1}{2} \times 28 \times 28 \times 1 \\
=\amp 392 \, \text{cm}^2
\end{align*}
Area of the segment is given by:
\begin{align*}
\text{Area of Segment} = \amp \text{Area of Sector} - \text{Area of Triangle} \\
=\amp 615.75 - 392 \\
=\amp 223.75 \, \text{cm}^2
\end{align*}
The area of the segment removed is \({\color{black}223.75 \,\text{cm}^2}\text{.}\)
Exercises Exercises
1.
2.
Subsection 3.1.5 Surface area of a cone
Activity 3.1.8.
Work in groups
Interactive work.
-
The figure below shows a cone, Play along with the interactive tool to understand the concept of a cone.
Figure 3.1.32. Area of a segment -
How many figure can you find in the above interactive tool?
-
You are provided with another interactive tool to explore the surface area of a cone.
Figure 3.1.33. Surface area of a cone Play along with the interactive tool to understand the concept of surface area of a cone. -
Before you start, make sure you understand the following terms:Base radius, Slant height, and Height.
-
Calculate the slant height in the above interactive tool.
-
Find the surface area of the cone in the interactive tool.Play along with the sliders, input boxes and coferm the surface area of the cone.
-
Discuss with your group members about the surface area of a cone and how it relates to real-life objects like ice cream cones, traffic cones, etc.
Definition 3.1.34.
A \(\textbf{cone}\) is a pyramid with a circular base.
A cone consists of a circular base and a curved surface that connects the base to the apex (the tip of the cone).
The \(\textbf{slant height}\) of a cone is the distance from the apex to any point on the edge of the base.
Key Takeaway
The surface area of the closed cone is given by:
\begin{equation*}
\pi r^2+ \pi r l
\end{equation*}
Where, where \(\pi r^2\) is area of the base and \(\pi r l\) the area of the curved surface. \(r\) is the radius of the cone and \(l\) is the slant height of the cone.
See the figure below.
Example 3.1.35.
Determine the surface area of the closed cone shown below.
Solution.
The surface area of the above figure is given by;
\(\text{SA}=\pi r^2 +\pi r l\)
\begin{align*}
\text{Circular base area}=\amp \pi r^2 \\
= \amp \frac{22}{7} \times 14 \times 14\\
= \amp 22 \times 2 \times 14 \\
= \amp 616 \, \text{m}^2
\end{align*}
\begin{align*}
\text{Curved surface area}=\amp \pi r l \\
= \amp \frac{22}{7} \times 14 \times 15\\
= \amp 22 \times 2 \times 15 \\
= \amp 660\, \text{m}^2
\end{align*}
Therefore, the total surface area is given by:
\begin{align*}
\text{Total surface area} = \amp 616\, \text{m}^2 + 660\, \text{m}^2\\
= \amp 1276\, \text{m}^2
\end{align*}
Example 3.1.36.
A conical container open at the top, is made of metal and has a base radius of \(10 \, \text{cm}\) and a slant height of \(18 \, \text{cm}\text{.}\) Determine the total metal sheet required to construct this container.
Solution.
The conical container has no Circular base therefore, the area is given by:
\(\text{Surface area} = \pi r l\)
Substitute the given values:
\begin{align*}
\text{Surface area} = \amp \frac{22}{7} \times 10 \times 18\\
= \amp \frac{22}{7} \times 180\\
= \amp 22 \times 25.714\\
= \amp 565.7\, \text{cm}^2
\end{align*}
Therefore, the total metal sheet required is \({\color{black}565.7\, \text{cm}^2}\text{.}\)
Example 3.1.37.
A cone is constructed with a base diameter of \(20 \, \text{mm}\) and a height of \(30 \, \text{mm}\) as shown below.
Solution.
-
The slant height is given by:\begin{align*} l^2= \amp b^2+h^2\\ l^2 =\amp (\frac{20}{2})+ 30^2\\ l= \amp \sqrt{10^2+30^2}\\ = \amp \sqrt{100 + 900} \\ = \amp \sqrt{1000} \\ =\amp 31.62\, \text{mm} \end{align*}Therefore, the slant height is approximately \({\color{black} 31.62\, \text{mm}}\text{.}\)
-
The total surface area is given by:\begin{align*} \text{TSA} =\amp \pi r^2 + \pi r l \\ = \amp \pi \times 10^2 + \pi \times 10 \times 31.62 \\ = \amp \pi \times 100 + \pi \times 316.2 \\ = \amp 314.16 + 993.61 \\ = \amp 1307.77\, \text{mm}^2 \end{align*}Therefore, the total surface area of the cone is \({\color{black}1307.77\, \text{mm}^2}\text{.}\)
Exercises Exercises
1.
2.
Subsection 3.1.6 Surface area of a sphere
Activity 3.1.9.
\(\textbf{Work in groups}\)
Instractions
-
Look at the sphere on your right hand side.
-
Measure the distance from the center of the sphere to its surface. What do you call this distance?
-
Calculate the area of the figure shown.
-
Discuss with your group how you might find the total surface area of the sphere.
\(\textbf{Extended Activity}\)
Activity 3.1.10.
Work in Groups
Play along with the interactive tool below to explore more about area of a \(\textbf{Sphere}\)
Definition 3.1.39.
A \(\textbf{sphere}\) is a solid that is entirely round with every point on the surface at anequal distance from the centre.
It’s defined as the set of all points in space that are equidistant from a central point.
The distance from the center to any point on the surface is called the \(\textbf{radius}\text{.}\)
Key Takeaway
Given the Shere of radius \(\huge{\textbf{r}}\) as shown below.
The surface area of a sphere is \({\color{black} 4 \pi r^2}\)
Example 3.1.40.
Find the surface area of a sphere whose diameter is \(21 \, \text{cm}\text{.}\)
Solution.
The diameter of the sphere is \(21 \, \text{cm}\text{,}\) so the radius \(r = \frac{21}{2} = 10.5\) cm.
The formula for the surface area of a sphere is:
\(\text{SA}= 4 \pi \text{r}^2\)
Therefore,
\begin{align*}
\text{SA}= \amp 4 \times \frac{22}{7} \times 10.5^2 \\
= \amp 4 \times \frac{22}{7} \times 110.25 \\
= \amp 4 \times 346.5 \\
= \amp 1386 \text{ cm}^2
\end{align*}
Therefore, the surface area of the sphere is \({\color{black}1386 \text{ cm}^2}\text{.}\)
Example 3.1.41.
Find the area of the figure below. Use \(\pi =3.142\)
Solution.
The radius of the sphere is \(21\, \text{m}\text{.}\)
The formula for the surface area of a sphere is: \(\text{SA} = 4 \pi r^2\)
Substituting the values:
\begin{align*}
\text{SA} = \amp 4 \times 3.142 \times 21^2\\
= \amp 4 \times 3.142 \times 441\\
= \amp 4 \times 1385.622\\
= \amp 5542.488 \text{ m}^2
\end{align*}
Therefore, the surface area of the sphere is \({\color{black}5542.49 \text{ m}^2}\text{.}\)
Example 3.1.42.
The balls used in a golf tournament have diameter of \(4.2 \text{cm}\) and \(4.4 \,\text{cm}\text{.}\) What is the difference in the surface area between the largest and smallest golf ball?
Solution.
The diameter of the smallest ball is \(4.2\,\text{cm}\text{,}\) so its radius is \(r_1 = \frac{4.2}{2} = 2.1\,\text{cm}\text{.}\)
The diameter of the largest ball is \(4.4\,\text{cm}\text{,}\) so its radius is \(r_2 = \frac{4.4}{2} = 2.2\,\text{cm}\text{.}\)
The formula for the surface area of a sphere is:
\begin{equation*}
\text{SA} = 4\pi r^2
\end{equation*}
For the smallest ball:
\begin{align*}
\text{SA}_1 = \amp 4 \times \pi \times (2.1)^2\\
= \amp 4 \times \pi \times 4.41\\
= \amp 17.64\pi
\end{align*}
For the largest ball:
\begin{align*}
\text{SA}_2 = \amp 4 \times \pi \times (2.2)^2\\
= \amp 4 \times \pi \times 4.84\\
= \amp 19.36\pi
\end{align*}
The difference in surface area is:
\begin{align*}
\text{Difference} = \amp 19.36\pi - 17.64\pi\\
= \amp 1.72\pi
\end{align*}
If \(\pi = 3.142\text{:}\)
\begin{align*}
\text{Difference} = \amp 1.72 \times 3.142\\
= \amp 5.40224\,\text{cm}^2
\end{align*}
Therefore, the difference in surface area between the largest and smallest golf ball is \({\color{black}5.40\,\text{cm}^2}\) .
Technology 3.1.43.
\(\textbf{Technology Integration: Exploring Area and Surface Area}\)
-
\(\textbf{BBC Bitesize Geometry and Measurement}\)This site offers short interactive lessons and videos on calculating areas and surface areas. Topics include sectors, pyramids, prisms, cones, and more, with quizzes to test your understanding.
-
\(\textbf{YouTube Shifting Grades and Anil Kumar Math}\)These channels provide clear and detailed explanations of how to find area and surface area of different shapes using step-by-step examples and real-life applications.
