Skip to main content
Contents Dark Mode Prev Up Next \(\newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Section 1.2 Cubes and cuberoots
A cube is a number means that a number is multiplied by itself three times.
Subsection 1.2.1 Methods for working out cubes
There are different ways of working out cubes of numbers. They include use of a calculator or a mathematical table.
Subsubsection 1.2.1.1 Finding cubes with a calculator
Use of a calculator is the easiest and fastest way to calculate cubes of numbers. A cube is simply
\(x^3\text{.}\) Where
\(x\) is any numerical value
While finding the cubes of number, always pay attention to the sign preceeding the number.
Activity 1.2.1 .
\(\textbf{Work in groups}\)
\(5\) Scientific calculators.
\(5\) Sheets of a paper having
\(3\) questions on each.
\(5\) Pens for recording result.
The teacher to give the
\(5\) calculators and
\(5\) sheets of paper, each containing the mentioned number of questions.
The teacher to demonstrate to the students how to power on the calculator and students to do the same.
Students to select in their groups a person to key in the given questions while the other record the results.
The groups to exchange their answer sheets and confirm the answers.
The teacher to cross check the answers.
Example 1.2.1 .
Whale was told to work out the cube of
\(9\text{.}\) What was his final answer?
Solution .
\begin{align*}
9\times 9\times 9 =\amp 729
\end{align*}
Example 1.2.2 .
A student is working out the cube of
\(6\text{.}\) What is the answer obtained?
Solution .
\begin{align*}
6\times 6\times 6 =\amp 216
\end{align*}
Subsubsection 1.2.1.2 Calculating cubes with a mathematical table
Mathematical table is a structured list of numerical data, often showing the results of calculations for different inputs.
Activity 1.2.2 .
\(\textbf{Work in groups}\)
Sheets of paper containing questions.
Under the teachers guidance, the learners to divide themselves in groups of
\(5\text{.}\)
Let each group pick question paper from the teacher.
Let the teacher pick a random question then demonstrate to the students how to read the value from the mathematical table.
Students in the groups to proceed with attempting the remaining questions.
The teacher to walk through the groups and validate the answers.
Students to submit the questions they found challenging and the whole class to participate in solving them.
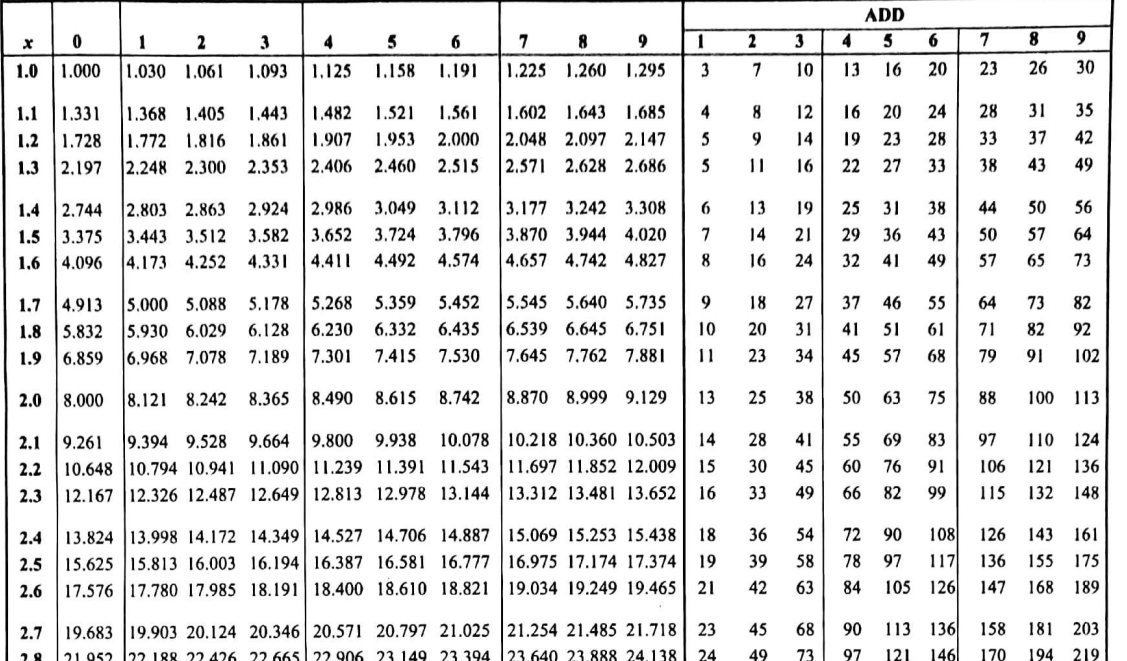
Example 1.2.3 .
Using the table below, calculate the cube of
\(2.0\) and
\(1.3\)
Solution .
Figure 1.2.4. Table for cubes
Move down along the column headed
\('x'\) and locate the number
\(2.0\text{.}\)
Move to the right along this row, where it intersects with the colum headed
\('0'\) in the second section.
Pick the next question
\(1.34\text{.}\) Move down along the column headed
\(x\) vertically and locate
\(1.3\)
Move horizontally on column headed
\(x\) to where
\(4\) is located and mark where it intersects with
\(1.3\text{.}\) The answer obtained is
\(2.406\)
Subsubsection 1.2.1.3 Working out cuberoots with a calculator
A calculator is also the fastest way of performing this operation. The cuberoot symbol is
\(\sqrt[3]{x}\text{.}\) Where
\(x\) is any number.
Activity 1.2.3 .
\(\textbf{Work in groups}\)
Sheet of paper containing questions
Under the teachers guidance, the learners to divide themselves in groups of
\(5\text{.}\)
Ask students to arrange the items into 3D cubes with equal length, width, and height.
Have students count how many items make one edge of the cube. That number is the cube root.
Teacher to provide groups with random numbers of items
\(50\) or
\(100\) to estimate the closest cube root.
Share results, talk about patterns, and relate cube roots to real-life 3D objects.
Example 1.2.5 .
A farmer packed
\(125, \text {oranges}\) into small square boxes. He wants to stack the boxes in the shape of a cube so that each side of the cube has the same number of boxes. How many boxes will be on one edge of the cube?
Solution .
\begin{gather*}
\sqrt[3]{125} = 5 \
\end{gather*}
Example 1.2.6 .
A farmer packed
\(1000, \text {guavas}\) into small square boxes. He wants to stack the boxes in the shape of a cube so that each side of the cube has the same number of boxes. How many boxes will be on one edge of the cube?
Solution .
\begin{gather*}
\sqrt[3]{1000} = 10\
\end{gather*}
Subsubsection 1.2.1.4 Working out cuberoots with a mathematical table
In this section, a mathematical table is used to calculate the given values
Activity 1.2.4 .
\(\textbf{Work in groups}\)
Under the teachers guidance, the learners to divide themselves in groups of
\(5\text{.}\)
Let each group pick question paper from the teacher.
Let the teacher pick a random question then demonstrate to the students how to read the value from the mathematical table.
Students in the groups to proceed with attempting the remaining questions.
The teacher to walk through the groups and validate the answers.
Students to submit the questions they found challenging and the whole class to participate in solving them.
Example 1.2.7 .
Using the table below, calculate the cuberoot of
\(27\) and
\(10.82\)
Solution .
Figure 1.2.8. Table for cubes
Using the table of cubes, locate
\(27\) in the middle section.
\(27\) is in the row header
\(3\) and column headed
\(0\)
Hence the cuberoot of
\(27\) is
\(3\)
For the second question, look for
\(10.82\text{.}\) Since it does not appear look for the number nearest to it that is
\(10.794\)
The number
\(10.794\) is in the row headed
\(2.2\) and the column headed
\(1\)
Find the difference between \(10.82\) and \(10.794\text{.}\) That is :
\begin{align*}
10.82-10.794 =\amp 0.026
\end{align*}
Move along the same row to the difference column and look for the number
\(26\)
Since
\(26\) does not appear, look for the closest number that is
\(30\)
Note the number at the head of the column where
\(30\) is located, combine it with
\(2.21\) to get
\(2.212\)
Technology 1.2.9 .
\(\textbf{Technology Integration: Working out of cubes and cube root}\)
\(\textbf{YouTube: Elimu TV }\)
This channel guides through the steps of working out cubes and cube roots using a mathematical table.