Skip to main content

Grade 9 Maths Book An Easy Way to Learn Maths

INNODEMS

Section 4.4 Trigonometry

Trigonometry is a branch of mathematics that studies the relationship between the angles of a right-angled triangle and the ratios of its sides.
🔗
These ratios are known as trigonometric ratios and they include sine, cosine and tangent
🔗

Subsection 4.4.1 Identifying Angles and Sides of Right Angled Triangles

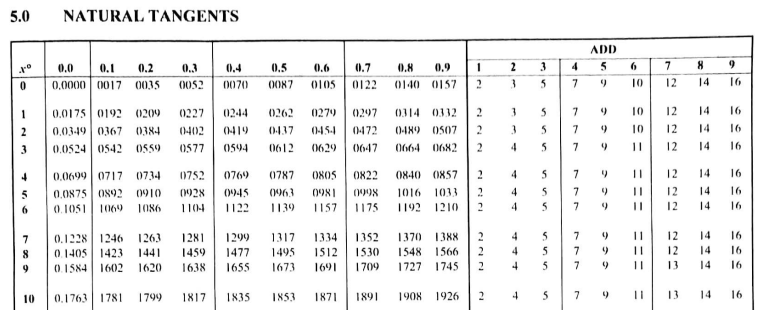
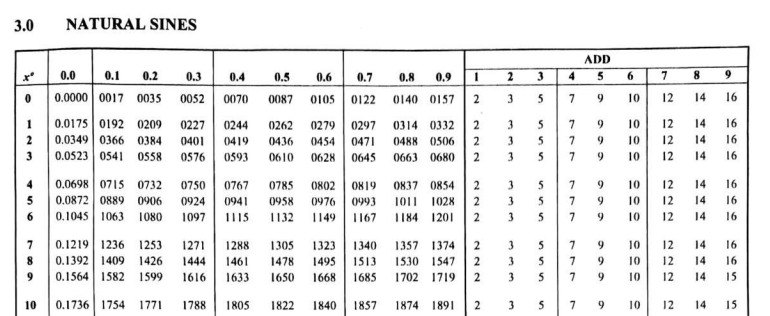
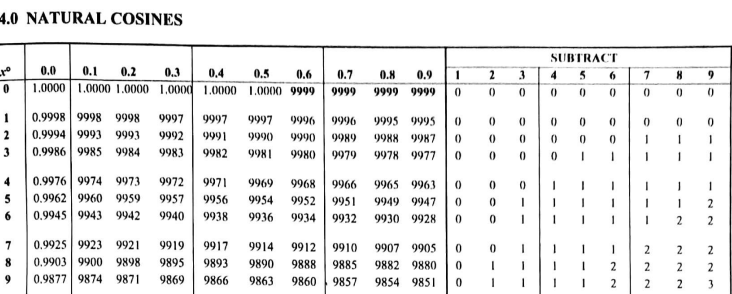
Activity 4.4.1.

\(\textbf{Work in groups}\)
🔗
  1. Draw a right-angled triangle and label its vertices as \(P\text{,}\) \(Q\text{,}\) and \(R\text{,}\) with the right angle positioned at \(P\text{.}\)
    🔗
    🔗
  2. Identify the side that is next to angle \(Q\text{,}\) excluding the hypotenuse.
    🔗
    🔗
  3. Point out the hypotenuse, the side that lies opposite the \(90\)° angle.
    🔗
    🔗
  4. Now repeat the same steps, but this time use angle \(R\) as your reference.
    🔗
    🔗
🔗
🔗
\(\textbf{Key Takeaway}.\)
🔗
  • A right-angled triangle always has one angle equal to \(90\)°. The other two angles must be acute angles
    🔗
    🔗
  • The sides that include the right angle are perpendicular to each other and the third side is called the hypotenuse.
    🔗
    🔗
  • If you are given an angle in a right-angled triangle, the side opposite to that angle is called the opposite side, while the side next to the angle (excluding the hypotenuse) is called the adjacent side as shown below.
    🔗
    🔗
🔗

Example 4.4.1.

The figure below shows a right-angled triangle \(PQR\text{.}\) Name the sides which are opposite and adjacent to the angle \(\theta\) and identify the hypotenuse side.
🔗
Solution.
Side \(PR\) is adjacent to angle \(\theta\text{.}\)
🔗
Side \(PQ\) is opposite to angle \(\theta\)
🔗
The hypotenuse is \(QR\text{.}\)
🔗
🔗
🔗
🔗

Subsection 4.4.2 Identifying Sine, Cosine and Tangent Ratios from a Right Angled Triangle

Subsubsection 4.4.2.1 Sine of an Acute Angle

Activity 4.4.2.
\(\textbf{Work in groups}\)
🔗
  1. In the figure below,\(AP\) and \(BQ\) are perpendicular to \(CR\) and \(\angle YOX=\theta\text{.}\)
    🔗
    🔗
  2. Measure the following sides of the triangles and record them in the table below.
    🔗
    Triangle Opposite Hypotenuse \(\frac{\textbf{Opposite}}{\textbf{Hypotenuse}}\)
    \(OAP\) \(AP= \) \(OP=\)
    \(OBQ\) \(BQ=\) \(OQ=\)
    \(OCR\) \(CR=\) \(OR=\)
    🔗
  3. What do you notice about the ratio \(\frac{\textbf{Opposite}}{\textbf{Hypotenuse}}\text{?}\)
    🔗
    🔗
  4. Share your findings with other groups in the class.
    🔗
    🔗
🔗
🔗
\(\textbf{Key Takeaway}.\)
🔗
The value of the ratio is constant in all triangles, regardless of the size of the triangle.
🔗
This constant value is obtained by taking the ratio of the side opposite the angle \(\theta\) to the hypotenuse side in each case.
🔗
This ratio is called the \(\textbf{sine}\) of the angle \(\theta\) and is denoted by \(\sin\theta\text{.}\)
🔗
In general, given a right-angled triangle \(ABC\) with angle \(\theta\) at vertex \(A\text{,}\)as shown in the figure below, the sine of angle \(\theta\) is defined as:
🔗
\(\sin\theta=\frac{\textbf{Opposite}}{\textbf{Hypotenuse}}=\frac{BC}{AC}\)
🔗
Example 4.4.2.
Determine the sine of angle \(\theta\) in the triangle below.
🔗
Solution.
\begin{align*} sin\,\theta=\amp \frac{\textbf{opposite}}{\textbf{hypotenuse}}\\ =\amp \frac{MN}{MO}\\ =\amp \frac{8}{MO} \end{align*}
🔗
Recall:
\begin{align*} MO^2=\amp 15^2+8^2 \\ =\amp 225+ 64\\ =\amp 289\\ MO= \amp 17\,cm \end{align*}
🔗
Thus,
\begin{align*} sin \,\theta= \amp \frac{8}{17}\\ =\amp 0.4706 \end{align*}
🔗
🔗
🔗
🔗

Subsubsection 4.4.2.2 Cosine of an Acute Angles

Activity 4.4.3.
\(\textbf{Work in groups}\)
🔗
  1. In the figure below,\(AP\)and \(BQ\) are perpendicular to \(CR\) and \(\angle YOX=\theta\text{.}\)
    🔗
    🔗
  2. Measure the following sides of the triangles and record them in the table below.
    🔗
    Triangle Adjacent Hypotenuse \(\frac{\textbf{Adjacent}}{\textbf{Hypotenuse}}\)
    \(OAP\) \(OA=\) \(OP=\)
    \(OBQ\) \(OB=\) \(OQ=\)
    \(OCR\) \(OC=\) \(OR=\)
    🔗
  3. What do you notice about the ratio \(\frac{Adjacent}{Hypotenuse}\text{?}\)
    🔗
    🔗
  4. Share your findings with other groups in the class.
    🔗
    🔗
🔗
🔗
Key Takeaway
🔗
The value of the ratio is constant in all triangles, regardless of the size of the triangle.
🔗
This constant value is obtained by taking the ratio of the side adjacent to the angle \(\theta\) to the hypotenuse side in each case.
🔗
This ratio is called the \(\textbf{cosine}\) of the angle \(\theta\) and is denoted by \(\cos\theta\text{.}\)
🔗
In general, given a right-angled triangle \(ABC\) with angle \(\theta\) at vertex \(A\text{,}\)as shown in the figure below, the cosine of angle \(\theta\) is defined as:
🔗
\(\cos\theta=\frac{\textbf{Adjacent}}{\textbf{Hypotenuse}}=\frac{AB}{AC}\)
🔗
Example 4.4.3.
Determine the cosine of angle \(\alpha\) in the triangle below.
🔗
Solution.
\begin{align*} cos\,\alpha=\amp \frac{\textbf{adjacent}}{\textbf{hypotenuse}}\\ =\amp \frac{8}{Hypotenuse} \end{align*}
🔗
Recall:
\begin{align*} Hyp^2=\amp 6^2+8^2 \\ =\amp 36+ 64\\ =\amp 100\\ Hyp= \amp 10\,cm \end{align*}
🔗
Thus,
\begin{align*} cos \,\alpha= \amp \frac{8}{10}\\ =\amp 0.8 \end{align*}
🔗
🔗
🔗
🔗

Subsubsection 4.4.2.3 Tangent of an Acute Angle

Activity 4.4.4.
\(\textbf{Work in groups}\)
🔗
  1. In the figure below,\(AP\)and \(BQ\) are perpendicular to \(CR\) and \(\angle YOX=\theta\text{.}\)
    🔗
    🔗
  2. Measure the following sides of the triangles and record them in the table below.
    🔗
    Triangle Opposite Adjacent \(\frac{\textbf{Opposite}}{\textbf{Adjacent}}\)
    \(OAP\) \(AP=-cm\) \(OA=-cm\)
    \(OBQ\) \(BQ=-cm\) \(OB=-cm\)
    \(OCR\) \(CR=-cm\) \(OC=-cm\)
    🔗
  3. What do you notice about the ratio \(\frac{\textbf{Opposite}}{\textbf{Adjacent}}\text{?}\)
    🔗
    🔗
  4. Share your findings with other groups in the class.
    🔗
    🔗
🔗
🔗
\(\textbf{Key Takeaway}.\)
🔗
The value of the ratio is constant in all triangles, regardless of the size of the triangle.
🔗
This constant value is obtained by taking the ratio of the side opposite to the angle \(\theta\) to the adjacent side in each case.
🔗
This ratio is called the \(\textbf{tangent}\) of the angle \(\theta\) and is denoted by \(\tan\theta\text{.}\)
🔗
In general, given a right-angled triangle \(ABC\) with angle \(\theta\) at vertex \(A\text{,}\)as shown in the figure below, the tangent of angle \(\theta\) is defined as:
🔗
\(\tan\theta=\frac{\textbf{Opposite}}{\textbf{Adjacent}}=\frac{BC}{AB}\)
🔗
Example 4.4.4.
Determine the cosine of angle \(\beta\) in the triangle below.
🔗
Solution.
\begin{align*} tan \,\beta= \amp \frac{Opposite}{Adjacent}\\ =\amp \frac{3}{4} \\ =\amp 0.75 \end{align*}
🔗
🔗
🔗
🔗
🔗

Subsection 4.4.3 Reading Tables of Trigonometric Ratios For Acute Angles

Subsubsection 4.4.3.1 Table of Tangents

Table of Natural Tangents
Activity 4.4.5.
\(\textbf{Work in pairs}\)
🔗
  1. Follow the steps below to read the table of natural tangents for acute angles.
    🔗
    (i) Identify the column headed \(x^\circ\)
    🔗
    (ii) Start from the top and move downwards till you reach \(5\text{.}\)
    🔗
    (iii) Move to the right in the row of \(5\) and reach the column headed \(0.2\)
    🔗
    (iv) Read the value in the cell where the row and column meet.
    🔗
    🔗
  2. Share your work with the class.
    🔗
    🔗
🔗
🔗
Example 4.4.5.
Use the table of natural tangents to find the value of the following angles.
🔗
(a) \(\tan 4.0^\circ\)
🔗
(b) \(\tan 3.2^\circ\)
🔗
(c) \(\tan 2.37^\circ\)
🔗
Solution.
(a) Go to tangent tables, look for angle \(4.0^\circ\text{,}\) and move to the column for \(0.0\text{.}\) The value is \(0.0699\text{.}\)
🔗
Therefore \(\tan 4.0^\circ = 0.0699\)
🔗
(b) Go to tangent tables, look for angle \(3^\circ\text{,}\) and move to the column for \(0.2\text{.}\) The value is \(0.0559\text{.}\)
🔗
Therefore \(\tan 3.2^\circ = 0.0559\)
🔗
(c) (i) Go to tangent tables, look for angle \(2^\circ\text{,}\) and move to the column for \(0.3\text{.}\) The value is \(0.0402\)
🔗
(ii) Move Horizontally to the right in the row of \(2.3\) and reach the column headed \(0.7\text{.}\) Read the number in the cell where the row and column meet and add to \(0.0419\text{.}\) The value is \(0.0402 + 0.0012 = 0.0414\)
🔗
Therefore \(\tan 2.37^\circ = 0.0414\)
🔗
🔗
🔗
🔗

Subsubsection 4.4.3.2 Table of Sines

Activity 4.4.6.
\(\textbf{Work in pairs}\)
🔗
  1. Follow the steps below to read the table of natural sines for acute angles.
    🔗
    (i) Look at the column headed \(x^\circ\)
    🔗
    (ii) Start from the top and move downwards till you reach \(5\text{.}\)
    🔗
    (iii) Move to the right in the row of \(5\) and reach the column headed \(0.2\)
    🔗
    (iv) Read the value in the cell where the row and column meet.
    🔗
    🔗
  2. Share your work with the class.
    🔗
    🔗
🔗
🔗
Example 4.4.6.
Use the table of natural sines to find the value of \(\sin 3.81^\circ\text{..}\)
🔗
Solution.
(i) Go to sine tables, look for angle \(3^\circ\text{,}\) and move to the column for \(0.8\text{.}\) The value is \(0.0663\text{.}\)
🔗
(ii) Move Horizontally to the right in the row of \(3.8\) and reach the column headed \(0.1\text{.}\) Read the number in the cell where the row and column meet and add to \(0.0523\text{.}\)i.e \(0.0663 + 0.0002 = 0.0665\)
🔗
Therefore \(\sin 3.81^\circ = 0.0665\)
🔗
🔗
🔗
🔗

Subsubsection 4.4.3.3 Table of Cosines

Activity 4.4.7.
\(\textbf{Work in pairs}\)
🔗
  1. Follow the steps below to read the table of natural cosines for acute angles.
    🔗
    (i) Look at the column headed \(x^\circ\)
    🔗
    (ii) Move down the column until you reach the row for \(4^\circ\text{.}\)
    🔗
    (iii) Move to the right in the row of \(4^\circ\) and reach the column headed \(0.0\text{.}\)
    🔗
    (iv) Read the value in the cell where the row and column meet.
    🔗
    🔗
  2. Share your work with the class.
    🔗
    🔗
🔗
🔗
Example 4.4.7.
Use cosine tables to find the value of the following angles.
🔗
(a) \(\cos 2.5^\circ\)
🔗
(b) \(\cos 3.24^\circ\)
🔗
Solution.
(a) (i) Go to cosine tables
🔗
(ii) Look for angle \(2^\circ\text{,}\) and move across to the column for \(0.5\text{.}\)
🔗
(iii) The value is \(0.9990\)
🔗
Therefore \(\cos 2.5^\circ = 0.9990\)
🔗
(b) (i) Go to cosine tables
🔗
(ii) Look for angle \(3^\circ\text{,}\) and move across to the column for \(0.2\text{.}\)
🔗
(iii) The value is \(0.9984\)
🔗
(iv) Move horizontally to the right in the row of \(3.2\) and reach the column headed \(0.4\text{.}\) Read the number in the cell where the row and column meet and subtract from \(0.9984\text{.}\)i.e \(0.9984 - 0.0000 = 0.9984\)
🔗
Therefore \(\cos 3.24^\circ = 0.9984\)
🔗
🔗
🔗
Example 4.4.8.
Use table to find the angle whose cosine is \(0.9962\text{.}\)
🔗
Solution.
🔗
🔗
🔗
🔗

Subsection 4.4.4 Determining Trigonometric Ratios of Acute Angles Using Calculators

Activity 4.4.8.

\(\textbf{Work in pairs}\)
🔗
  1. Use a scientific calculator to find the values of the following trigonometric ratios for the given angles. Ensure your calculator is set to degrees mode.
    🔗
    Angle\(\theta\) \(\sin \theta\) \(\cos \theta\) \(\tan \theta\)
    \(15^\circ\)
    \(30^\circ\)
    \(45^\circ\)
    \(60^\circ\)
    \(75^\circ\)
    \(90^\circ\)
    🔗
  2. Follow the steps below to determine the value of \(\sin 30^\circ\text{.}\)
    🔗
    (i) Press the \(\sin\) button on your calculator.
    🔗
    (ii) Enter the angle \(30\) using the number keys.
    🔗
    (iii) Press the \((=)\) button to calculate the value.
    🔗
    🔗
  3. Follow the same steps to find all other trigonometric ratios in the table.
    🔗
    🔗
  4. Share your results with the class and compare the values you obtained.
    🔗
    🔗
🔗
🔗

Example 4.4.9.

Calculate the value of each of the following using your calculator, giving your answers correct to 4 significant figures:
🔗
(a) \(\sin 25^\circ\)
🔗
(b) \(\tan 50^\circ \)
🔗
(c) \(\cos 70^\circ\)
🔗
Solution.
(a) \(\sin 25^\circ \)
🔗
press the \(\sin\) button, enter \(25\text{,}\) and then press \((=)\text{.}\) The calculator displays: \(0.42261826\)
🔗
Therefore, the value of \(\sin 25^\circ\) is \(0.4226\text{.}\)
🔗
(b) \(\tan 50^\circ\)
🔗
press the \(\tan\) button, enter \(50\text{,}\) and then press \((=)\text{.}\) The calculator displays: \(1.19175359\)
🔗
Therefore, the value of \(\tan 50^\circ\) is \(1.1918\text{.}\)
🔗
(c) \(\cos 70^\circ\)
🔗
press the \(\cos\) button, enter \(70\text{,}\) and then press \((=)\text{.}\) The calculator displays: \(0.34202014\)
🔗
Therefore, the value of \(\cos 70^\circ\) is \(0.3420\text{.}\)
🔗
🔗
🔗

Example 4.4.10.

Use a calculator to find the angle whose sine is \(0.8660\)
🔗
Solution.
(i) press the shift key followed by the sin key to get sin⁻¹.
🔗
(ii) enter \(0.8660\) and press the \((=)\) button. The calculator displays: \(60\)
🔗
Therefore, the angle whose sine is \(0.8660\) is \(60^\circ\text{.}\)
🔗
🔗
🔗
🔗

Subsection 4.4.5 Applying Trigonometric Ratios To Calculate Lengths and Angles of Right Angled- Triangles

Activity 4.4.9.

\(\textbf{Work in pairs}\)
🔗
  1. Use cosines to find the size of angle \(\alpha\) in the right-angled triangle below.
    🔗
    🔗
  2. Follow the steps below;
    🔗
    (i) Identify the side that is adjacent to angle \(\alpha\) .
    🔗
    (ii) Identify the hypotenuse of the triangle.
    🔗
    Determine the cosine ratio of angle \(\alpha\) using the formula: \(\cos \alpha = \frac{\textbf{adjacent}}{\textbf{hypotenuse}}\)
    🔗
    (iii) Use table of cosines or a calculator to find the value of angle \(\alpha\) using the cosine ratio you calculated.
    🔗
    🔗
  3. Share your findings with other groups.
    🔗
    🔗
🔗
🔗

Example 4.4.11.

Determine the length of the side marked \(y\) in the right-angled triangle below to the nearest \(4\) significant figures.
🔗
Solution.
\begin{align*} \sin \theta= \amp \frac{\textbf{Opposite}}{\textbf{Hypothenuse}}\\ \amp\sin 69^\circ = \frac{y}{10}\\ y= \amp 10 \sin 69^\circ \\ y= \amp 0.93358043\\ y= \amp 9.335 \text{ cm} \end{align*}
🔗
🔗
🔗
🔗
🔗
PrevTopNext